На практике часто сталкиваемся с ситуацией, когда результат опыта описывается несколькими случайными величинами. Например, при стрельбе по плоской мишени, отклонение от центра задается двумя случайными величинами: абсциссой и ординатой точки 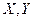 . Свойства системы не исчерпываются свойствами отдельных случайных величин, есть еще взаимные связи (зависимости) между случайными величинами. Для описания системы удобно использовать геометрическую интерпретацию:
. Свойства системы не исчерпываются свойствами отдельных случайных величин, есть еще взаимные связи (зависимости) между случайными величинами. Для описания системы удобно использовать геометрическую интерпретацию: 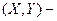 случайный вектор.
случайный вектор.
Закон распределения системы случайных величин – это соотношение, устанавливающее связь между областями возможных значений случайных величин и вероятностями появления случайного вектора в этих областях.
Определение. Функцией распределения случайного вектора или функцией совместного распределения случайных величин 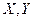 называется функция двух действительных переменных
называется функция двух действительных переменных 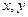 , определяемая соотношением:
, определяемая соотношением:
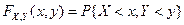 .
.
Обозначим через:
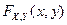 - функцию распределения системы
- функцию распределения системы  ;
;
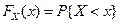 - функцию распределения случайной величины
- функцию распределения случайной величины  ;
;
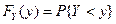 - функцию распределения случайной величины
- функцию распределения случайной величины  .
.
Функция распределения 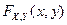 обладает следующими свойствами:
обладает следующими свойствами:
1. 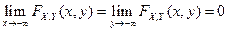 .
.
2. 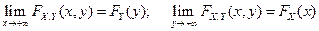 .
.
3. 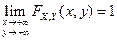 .
.
4. Функция 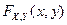 - неубывающая функция по каждому из аргументов.
- неубывающая функция по каждому из аргументов.
5. Функция 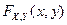 непрерывна слева по каждому из аргументов.
непрерывна слева по каждому из аргументов.
Свойство 2 обычно называют условием согласованности. Оно означает, что функции распределения отдельных случайных величин могут быть найдены предельным переходом из функции совместного распределения этих величин.
Вероятность попадания случайного вектора в прямоугольник со сторонами, параллельными координатным осям, т.е. вероятность выполнения неравенств 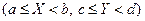 , может быть найдена с помощью функции распределения системы:
, может быть найдена с помощью функции распределения системы:
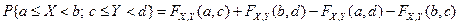 .
.
Определение. Случайный вектор 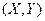 называется вектором дискретного типа, если множество его значений, т.е. пар
называется вектором дискретного типа, если множество его значений, т.е. пар 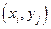 , конечное или счетное. Если перечислить всевозможные пары значений случайного вектора и сопоставить каждой паре вероятность
, конечное или счетное. Если перечислить всевозможные пары значений случайного вектора и сопоставить каждой паре вероятность 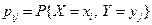 , причем
, причем 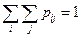 , то получим закон распределения дискретного случайного вектора.
, то получим закон распределения дискретного случайного вектора.
Законы распределения случайных величин 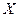 и
и  выражаются через вероятности
выражаются через вероятности 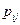 следующим образом:
следующим образом:
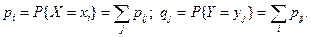
Определение. Случайный вектор 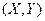 называется вектором непрерывного типа, если функция распределения
называется вектором непрерывного типа, если функция распределения 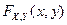 непрерывна на всей плоскости, и существует такая неотрицательная, интегрируемая функция
непрерывна на всей плоскости, и существует такая неотрицательная, интегрируемая функция 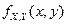 , называемая плотностью распределения системы, что
, называемая плотностью распределения системы, что
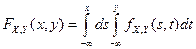 .
.
Свойства плотности распределения системы непрерывных случайных величин:
1. 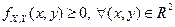 .
.
2. 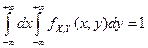 (условие нормировки).
(условие нормировки).
3. Если 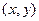 - точка непрерывности
- точка непрерывности 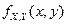 , то
, то 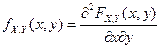 .
.
4. Плотности распределения вероятностей отдельных компонент случайного вектора выражаются в виде интегралов от совместной плотности:
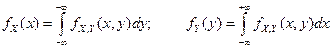 .
.
5. Вероятность попадания случайного вектора в произвольную квадрируемую область В на плоскости определяется по формуле:
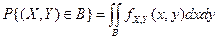 .
.
 2015-04-01
2015-04-01 2609
2609
