Проверка статистических гипотез. Во многих случаях результаты наблюдений используются для проверки предположений (гипотез) относительно тех или иных свойств распределения генеральной

Во многих случаях результаты наблюдений используются для проверки предположений (гипотез) относительно тех или иных свойств распределения генеральной совокупности.

Определение. Статистической гипотезой Н называется предположение относительно параметра или вида распределения изучаемой случайной величины Х.

Если распределение случайной величины Х известно, а по выборке наблюдений проверяют гипотезы о значении параметров распределения, то такие гипотезы называют параметрическими. Если же проверяются гтпотезы о виде самого распределения, то такие гипотезы называются непараметрическими.

Определение. Проверяемая гипотеза называется нулевой гипотезой и обозначается 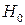. Наряду с гипотезой 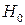рассматривают одну из альтернативных (конкурирующих) гипотез .

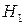Например, если проверяется гипотеза о том, что параметр 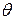равен некоторому заданному значению 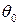, т.е. 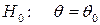, тогда в качестве альтернативной гипотезы могут быть взяты следующие:

.

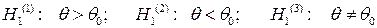Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.

Определение. Правило, по которому принимается решение принять или отклонить гипотезу 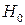, называется критерием К.

Решение признать или отклонить гипотезу, принимается на основе выборки наблюдений за случайной величиной Х. Поэтому, необходимо иметь некоторую подходящую статистику, называемую в этом случае статистикой Z критерия К.

Критерий К задают с помощью критического множества 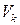, которое является подмножеством множества значений статистики Z.

Решение принимают следующим образом:

1) если выборочное значение статистики 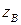принадлежит критическому множеству (критической области), то отвергают нулевую гипотезу 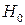и принимают альтернативную гипотезу ;

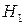2) если выборочное значение статистики 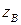не принадлежит критическому множеству 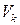(то есть принадлежит дополнению 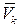множества 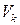до множества значений статистики Z), то отвергают альтернативную гипотезу 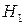и принимают нулевую гипотезу .

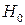При использовании любого критерия возможны ошибки следующих видов:

· принять гипотезу 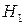, если верна 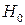- ошибка первого рода;

· принять гипотезу 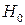, если верна 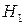- ошибка второго рода.

Вероятности совершения ошибок первого и второго рода обозначаются соответственно, 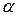и :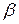

, ,

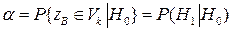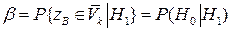где 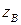- выборочное значение статистики Z,

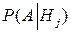- вероятность события А при условии, что справедлива гипотеза .

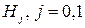Определение. Вероятность 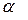называют уровнем значимости критерия и фиксируют перед анализом выборки. Как правило, .

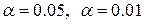Определение. Величину (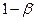), которая равна вероятности отвергнуть нулевую гипотезу, если она верна,называют мощностью критерия.

Отметим, что при заданном объеме выборки нельзя одновременно уменьшить 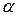и , и 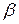. Как правило, уровень значимости критерия задают заранее, а критическую область следует выбирать таким образом, чтобы величина 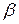была минимальна.

Таким образом, проверка параметрической статистической гипотезы при помощи критерия значимости может быть разбита на следующие этапы:

1) сформулировать проверяемую (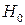) и альтернативную (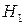) гипотезы;

2) назначить уровень значимости ;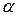

3) выбрать статистику Z критерия для проверки гипотезы ;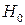

4) определить выборочное распределение статистики Z при условии, что верна гипотеза ;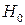

5) в зависимости от формулировки альтернативной гипотезы определить критическую область 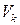одним из неравенств 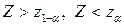или совокупностью неравенств 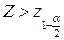и ;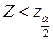

6) получить выборку наблюдений и вычислить выборочное значение 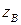статистики критерия;

7) принять статистическое решение:

· если 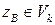, то отклонить гипотезу 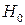, как не согласующуюся с результатами наблюдений;

· если 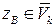, то принять гипотезу 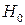, то есть считать, что она не противоречит результатам наблюдений.

Для проверки гипотез о параметрах нормально распределенной генеральной совокупности используются следующие статистики.

Пример. Проверим гипотезу о том, что генеральная средняя нормально распределенной совокупности равна заданному числу .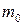

Для проверки этой гипотезы при известной дисперсии 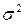следует использовать статистику: ,

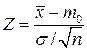которая имеет нормальное распределение спараметрами: 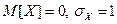(обозначается );

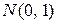если дисперсия генеральной совокупности неизвестна, то статистику:

,

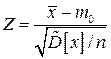которая имеет распределение Стьюдента с 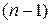степенью свободы.

Здесь 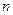- объем выборки,

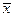- выборочное среднее,

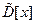- выборочная дисперсия,

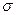- известное среднеквадратичное отклонение,

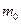- заданное число.

Задача. Пусть из нормально распределенной генеральной совокупности

а) с известной дисперсией ,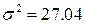

б) с неизвестной дисперсией

извлечена выборка объема 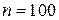и найдена выборочная средняя 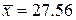. Требуется при уровне значимости 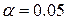проверить нулевую гипотезу 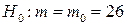(здесь - генеральная средняя), если конкурирующая гипотеза .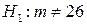

Решение. а) Поскольку дисперсия генеральной совокупности известна, выбираем статистику критерия 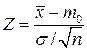, имеющую распределение .

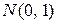Вычислим наблюдаемое (выборочное) значение статистики критерия -

.

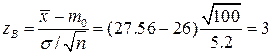Так как альтернативная гипотеза 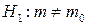, то критическую область следует взять двухсторонней, она задается неравенствам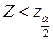и: и .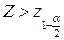

Плотность нормального распределения симметрична, значит, критическая область будет задана неравенством: .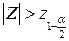

Таким образом, 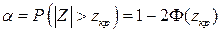, (здесь 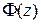- функция Лапласа) отсюда .

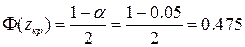По таблице значений функции Лапласа (приложение 1) находим .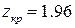

Так как 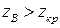(3 > 1.96), то выборочное значение статистики критерия попадает в критическую область, значит нулевую гипотезу отвергаем. Выборочное среднее и математическое ожидание генеральной совокупности различаются значимо.

б) Если дисперсия неизвестна, то в качестве статистики критерия возьмем статистику 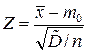, которая имеет распределение Стьюдента с 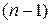степенью свободы.

Плотность распределения Стьюдента нечетная функция, 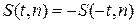, поэтому критическая область определяется неравенством

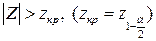. Тогда ,

.

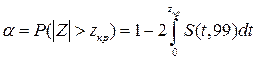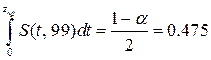По таблице квантилей распределения Стьюдента (приложение 2) находим 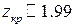, следовательно, вывод тот же, что и в предыдущем случае а).

Пример. Проверим гипотезу о том, что генеральная дисперсия нормально распределенной совокупности равна заданному значению .

Обозначим через n объем выборки, по которой найдена несмещенная дисперсия .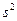

Для того, чтобы при заданном уровне значимости 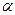проверить нулевую гипотезу 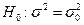о равенстве неизвестной генеральной дисперсии 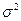гипотетическому (предполагаемому) значению при конкурирующей гипотезе 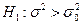, надо вычислить наблюдаемое значение статистики критерия 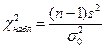, которая имеет распределение 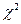с 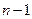степенью свободы. По таблице критических точек распределения 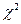, по заданному уровню значимости 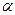и числу степеней свободы 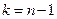находим критическую точку 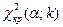. Если 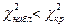- нулевая гипотеза принимается, если 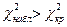- нулевую гипотезу отвергают.

Задача. Из нормальной генеральной совокупности извлечена выборка объема 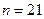и по ней найдена выборочная дисперсия 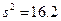. Требуется при уровне значимости 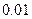проверить нулевую гипотезу 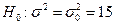, приняв в качестве конкурирующей гипотезы .

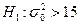Решение. Найдем наблюдаемое значение критерия: 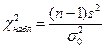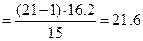. По условию, конкурирующая гипотеза имеет вид 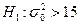, поэтому критическая область – правосторонняя. По приложению 3, по уровню значимости 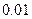и числу степеней свободы 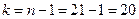находим критическую точку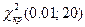 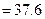. Так как 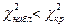- нулевая гипотеза принимается, т.е. различие между выборочной дисперсией 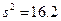и предполагаемой генеральной дисперсией 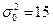незначимо.

Для проверки непараметрических гипотез также найден ряд подходящих статистик.

Пример. Проверим гипотезу о том, что генеральная совокупность имеет нормальное распределение.

Пусть эмпирическое распределение задано в виде последовательностиравноотстоящих вариант и соответствующих им частот: .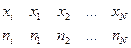

Гипотезу можно проверить с помощью критерия Пирсона, в котором используют статистику: ,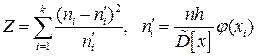

где n – объем выборки, h – шаг, равный разности между соседними вариантами, 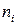- наблюдаемая частота, 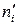- теоретическая частота, 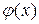- плотность нормального распределения .

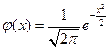Статистика Z имеет 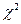(хи-квадрат) распределение с 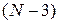степенями свободы (при условии, что математическое ожидание и дисперсия генеральной совокупности неизвестны).

Для проверки гипотезы при заданном уровне значимости 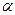, надо:

1. Вычислить выборочную среднюю 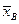и выборочную дисперсию .

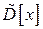2. Вычислить теоретические частоты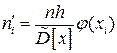

3. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:

а) составляют расчетную таблицу, по которой находят наблюдаемое значение критерия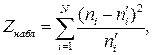

б) по таблице критических точек распределения 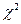, по заданному уровню значимости 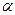и числу степеней свободы 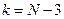находят критическую точку 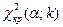правосторонней критической области.

Если 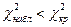, то нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно).

Если 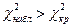- гипотезу отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо.

Задача. Используя критерий Пирсона, при уровне значимости 0,01 установить, случайно или значимо расхождение между эмпирическими частотами 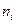и теоретическими частотами 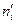, которые вычислены, исходя из гипотезы о нормальном распределении генеральной совокупности : .

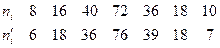Решение. Найдем наблюдаемое значение статистики критерия Пирсона: 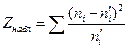. Составим расчетную таблицу:

			-
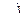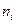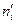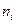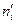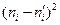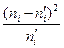					0,667
			-2		0,222
					0,444
			-4		0,211
			-3		0,231
					-
					1,286
S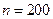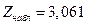

Из таблицы видно, что наблюдаемое значение критерия: 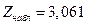. По таблице критических точек распределения 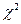, по уровню значимости 0,01 и числу степеней свободы 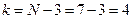(приложение 3) находим критическую точку правосторонней критической области 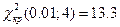. Так как 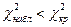, то нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности, т.е. расхождение между эмпирическими и теоретическими частотами незначимо (случайно).

Отметим, что если вариационный ряд непрерывный, то весь интервал изменения случайной величины Х разбивают на 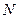промежутков одинаковой длины, и в качестве новых вариант берут середины интервалов: 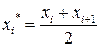. Затем нормируют случайную величину Х, то есть переходят к новой случайной величине 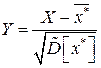и находят теоретические частоты 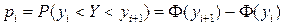, где 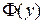- функция Лапласа. При этом наименьшее значение Y приравнивают к 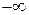, а наибольшее – к .

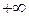Статистика 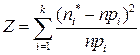, 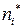- сумма частот, попавших в i - интервал, имеет также 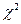-распределение с 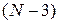степенями свободы. Затем вычисляют выборочное значение статистики критерия Пирсона и по таблице квантилей 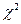-распределения находят критическое значение статистики 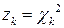, соответствующее заданному уровню значимости и числу степеней свободы. Если 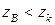, то гипотеза о нормальном распределении генеральной совокупности принимается, в противном случае гипотеза отвергается.