Точечная оценка дает приближенное значение параметра, однако в ряде задач требуется более строгое решение, а именно, желательно знать, что ошибка полученной оценки не выйдет за определенные пределы. Это особенно важно при малом числе наблюдений.
Пусть для параметра 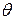 получена несмещенная оценка
получена несмещенная оценка 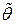 . Зададим некоторую, достаточно большую вероятность
. Зададим некоторую, достаточно большую вероятность 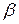 (0.9, 0.95, 0.99) и найдем число
(0.9, 0.95, 0.99) и найдем число 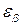 из условия:
из условия: 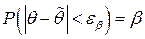 или
или 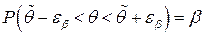 .
.
Это означает, что с вероятностью 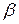 неизвестное значение параметра
неизвестное значение параметра 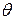 попадет в интервал
попадет в интервал 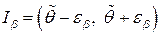 .
.
Замечание. Подчеркнем, что неизвестное значение параметра 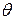 неслучайно, а интервал
неслучайно, а интервал 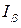 - случаен. То есть
- случаен. То есть 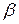 - вероятность того, что случайный интервал
- вероятность того, что случайный интервал 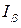 накроет неслучайное, неизвестное значение параметра
накроет неслучайное, неизвестное значение параметра 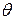 .
.
Определение. Число 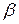 называют доверительной вероятностью,
называют доверительной вероятностью, 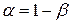 - уровнем значимости,
- уровнем значимости, 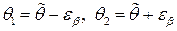 - доверительными границами,
- доверительными границами, 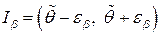 - доверительным интервалом.
- доверительным интервалом.
Замечание. Часто применяют односторонние доверительные интервалы, границы которых определяются из условий 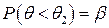 или
или 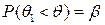 .
.
Замечание. Подчеркнем, что задача нахождения границ доверительного интервала для параметра 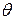 достаточно сложна. Для построения этого интервала, необходимо знать закон распределения оценки (статистики
достаточно сложна. Для построения этого интервала, необходимо знать закон распределения оценки (статистики 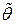 ), который может зависеть и от неизвестного параметра
), который может зависеть и от неизвестного параметра 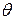 , и от закона распределения случайной величины Х. В ряде случаев удается перейти от статистики
, и от закона распределения случайной величины Х. В ряде случаев удается перейти от статистики 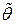 к некоторой другой статистике, закон распределения которой зависит от закона распределения случайной величины Х, числа опытов, но не зависит от неизвестных параметров.
к некоторой другой статистике, закон распределения которой зависит от закона распределения случайной величины Х, числа опытов, но не зависит от неизвестных параметров.
Основные результаты математической статистики получены для распределения статистик, построенных по выборке из нормально распределенной генеральной совокупности.
Пример. Найти доверительные интервалы для математического ожидания и дисперсии нормально распределенной случайной величины по результатам наблюдений с доверительной вероятностью 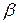 .
.
Решение. Для того, чтобы найти доверительный интервал для математического ожидания, используется статистика: 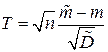 ,
,
где 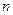 - число элементов в выборке;
- число элементов в выборке;
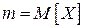 - неизвестный параметр – математическое ожидание случайной величины;
- неизвестный параметр – математическое ожидание случайной величины;
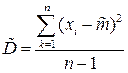 - несмещенная выборочная дисперсия;
- несмещенная выборочная дисперсия;
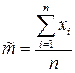 - выборочное среднее.
- выборочное среднее.
Данная статистика имеет распределение Стьюдента с 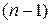 степенями свободы.
степенями свободы.
Замечание. Пусть задана случайная величина  , для которой известна функция распределения
, для которой известна функция распределения 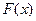 . Квантилью порядка р, называется число
. Квантилью порядка р, называется число 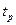 , удовлетворяющее уравнению:
, удовлетворяющее уравнению: 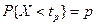 . Это уравнение равносильно следующему:
. Это уравнение равносильно следующему: 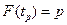 . Как правило, квантили часто используемых распределений приведены в таблицах.
. Как правило, квантили часто используемых распределений приведены в таблицах.
Для нахождения доверительного интервала используем условие:
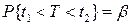 .
. 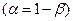
Решим неравенство: 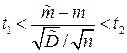 относительно
относительно 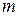 ; получим:
; получим:
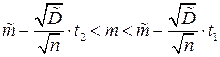 .
.
Плотность распределения Стьюдента - четная функция, поэтому доверительный интервал выбирают симметричным: 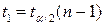 ;
; 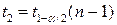 , здесь в качестве концов интервала используют квантили порядка
, здесь в качестве концов интервала используют квантили порядка 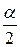 и (
и (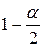 ) распределения Стьюдента с
) распределения Стьюдента с 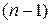 степенями свободы (эти квантили находим по приложению 2). Квантили этого распределения удовлетворяют условию:
степенями свободы (эти квантили находим по приложению 2). Квантили этого распределения удовлетворяют условию: 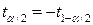 ; поэтому доверительный интервал для математического ожидания можно записать в виде:
; поэтому доверительный интервал для математического ожидания можно записать в виде:
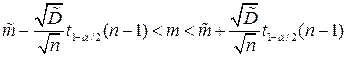 .
.
Для того, чтобы найти доверительный интервал для дисперсии нормально распределенной случайной величины, используется статистика:
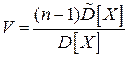 , которая имеет распределение
, которая имеет распределение 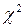 (хи-квадрат) с
(хи-квадрат) с 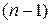 степенями свободы. Доверительный интервал будем искать из условия:
степенями свободы. Доверительный интервал будем искать из условия:
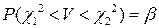 .
.
Решим неравенство: 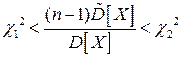 относительно неизвестного значения
относительно неизвестного значения 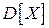 , получим:
, получим:
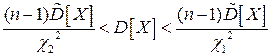 .
.
Плотность распределения случайной величины 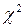 несимметричная функция (
несимметричная функция (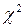 принимает только положительные значения), поэтому доверительный интервал выбираем так, чтобы вероятность выхода случайной величины
принимает только положительные значения), поэтому доверительный интервал выбираем так, чтобы вероятность выхода случайной величины 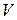 за пределы интервала слева и справа была одинакова:
за пределы интервала слева и справа была одинакова: 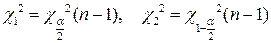 , т.е. концами интервала являются квантили порядка
, т.е. концами интервала являются квантили порядка 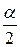 и
и 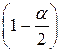 распределения
распределения 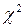 с
с 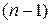 степенями свободы (значения этих квантилей находим по приложению 3).
степенями свободы (значения этих квантилей находим по приложению 3).
Таким образом, доверительный интервал для дисперсии имеет вид:
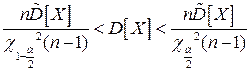 .
.
 2015-04-01
2015-04-01 924
924








