Зная эмпирическую функцию распределения, мы можем оценить характер теоретической функции распределения генеральной совокупности. Однако как в теории, так и на практике бывает важно оценить отдельные свойства случайной величины на основе экспериментальных данных.
Распределение случайной величины Х характеризуется целым рядом параметров или числовых характеристик, например: математическое ожидание, дисперсия, мода и так далее. Используя выборку исследуемой случайной величины, можно вычислить приближенные значения каждого из неизвестных параметров, называемые в статистике точечными оценками параметров (т.е. оценивание параметра осуществляется одним числом, точкой на числовой оси).
Точечные оценки параметров распределения являются значениями некоторых функций элементов выборки, которые называются статистиками. Например, для оценки математического ожидания случайной величины Х используют статистику 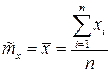 , которая называется выборочное среднее.
, которая называется выборочное среднее.
Оценку параметра 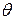 будем обозначать символом с тильдой:
будем обозначать символом с тильдой: 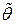 .
.
Очевидно, что значения статистик изменяются от выборки к выборке случайным образом, т.е. статистики являются случайными величинами. Для оценки данного параметра можно использовать несколько разных статистик, получая при этом различные значения оценок. Очевидно, что для наилучшей оценки следует взять такую статистику, значения которой для различных выборок из данной генеральной совокупности были бы «в среднем» близки к истинному значению параметра, который оценивается.
Качество оценок характеризуют следующими свойствами.
· Оценка 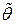 называется несмещенной, если ее математическое ожидание равно оцениваемому параметру:
называется несмещенной, если ее математическое ожидание равно оцениваемому параметру: 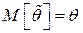 .
.
· Оценка 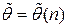 называется состоятельной, если при увеличении объема выборки
называется состоятельной, если при увеличении объема выборки 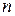 оценка
оценка 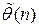 сходится по вероятности к
сходится по вероятности к 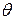 . Это означает, что для любых
. Это означает, что для любых 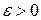 и
и 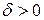 существует
существует 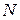 такое, что при
такое, что при 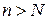 выполняется неравенство:
выполняется неравенство: 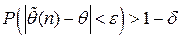 (вероятность того, что оценка
(вероятность того, что оценка 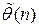 отличается от истинного значения
отличается от истинного значения 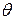 не больше, чем на
не больше, чем на 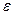 , близка к единице).
, близка к единице).
· Пусть 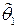 и
и 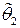 - две различные несмещенные оценки параметра
- две различные несмещенные оценки параметра 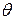 . Если
. Если 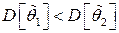 , то говорят, что оценка
, то говорят, что оценка 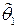 , более эффективна, чем оценка
, более эффективна, чем оценка 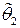 .
.
· Пример. Несмещенной и состоятельной оценкой математического ожидания 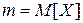 случайной величины Х будет выборочное среднее:
случайной величины Х будет выборочное среднее: 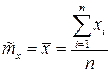 ,
,
а несмещенной и состоятельной оценкой дисперсии 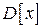 будет исправленная выборочная дисперсия:
будет исправленная выборочная дисперсия: 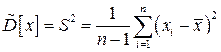 .
.
 2015-04-01
2015-04-01 509
509








