1. Решить задачу (таблица 6).
2. Решить задачу с использованием формулы Бернулли (таблица 7).
3. По заданной плотности распределения найти требуемые величины (табл. 8).
4. По сгруппированным данным построить гистограмму относительных частот
(таблица 9).
5.Проверить нулевую гипотезу о том, что заданное значение 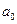 является математическим ожиданием нормально распределенной случайной величины при 5% уровне значимости для двусторонней критической области, если в результате обработки выборки объема
является математическим ожиданием нормально распределенной случайной величины при 5% уровне значимости для двусторонней критической области, если в результате обработки выборки объема 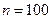 получено выборочное среднее
получено выборочное среднее 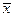 , а несмещенное квадратичное отклонение равно
, а несмещенное квадратичное отклонение равно 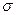 (таблица 10).
(таблица 10).
6. Найти выборочное уравнение линейной регрессии  на
на  на основании корреляционной таблицы (таблица 11).
на основании корреляционной таблицы (таблица 11).
6.1. Пример выполнения контрольной работы № 2. Вариант № 0.
1. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность того, что извлекли два разноцветных шара?
Решение. Эксперимент состоит в извлечении двух шаров из пятнадцати. Выбор осуществляется без возвращения, порядок извлеченных шаров не играет роли. Элементарным исходом является пара объектов вида: номер шара и его цвет, например: (первый белый, третий черный). Количество таких исходов 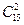 . Рассмотрим среди них исходы, благоприятствующие событию А={извлекли два разноцветных шара}. Количество способов выбрать один белый шар из 5 равно
. Рассмотрим среди них исходы, благоприятствующие событию А={извлекли два разноцветных шара}. Количество способов выбрать один белый шар из 5 равно 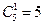 , количество способов выбрать один черный шар из 10 равно
, количество способов выбрать один черный шар из 10 равно 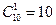 . Таким образом, количество благоприятствующих исходов
. Таким образом, количество благоприятствующих исходов 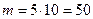 . Воспользуемся формулой классической вероятности:
. Воспользуемся формулой классической вероятности: 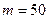 , а
, а 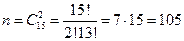 . Следовательно,
. Следовательно, 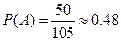 .
.
Ответ. 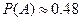 .
.
2. Вероятность того, что расход электроэнергии в течение одних суток не превысит установленной нормы, равна 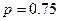 . Найти вероятность того, что в ближайшую неделю расход электроэнергии не превысит нормы в течении 4 суток.
. Найти вероятность того, что в ближайшую неделю расход электроэнергии не превысит нормы в течении 4 суток.
Решение. Эксперимент состоит в том, что в течение 7 дней наблюдают за расходом электроэнергии. Вероятность нормального расхода электроэнергии в продолжении каждых суток в неделю постоянна и равна 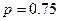 . Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна
. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна 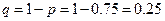 . Искомое событие: А={ровно 4 раза в течении 7 дней расход электроэнергии будет нормальным}.
. Искомое событие: А={ровно 4 раза в течении 7 дней расход электроэнергии будет нормальным}.
Используя формулу Бернулли, получаем:
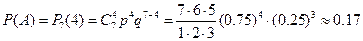 . Ответ.
. Ответ. 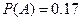 .
.
3. Задана плотность распределения непрерывной случайной величины 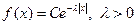 - параметр распределения.
- параметр распределения.
Найти нормировочную константу С, функцию распределения F(x), математическое ожидание M[X], дисперсию D[X].
 2015-04-01
2015-04-01 641
641








