Если функция f(x) – бесконечное число раз непрерывно дифференцируемая, то она может быть разложена в степенной ряд по формуле:
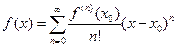 .
.
Этот ряд называется рядом Тейлора для функции f(x) (если разложение в точке 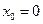 , то ряд называется рядом Маклорена). В области сходимости сумма этого ряда совпадает с функцией f(x).
, то ряд называется рядом Маклорена). В области сходимости сумма этого ряда совпадает с функцией f(x).
При разложении функции в степенной ряд можно использовать общую формулу или известные разложения основных элементарных функций в ряд Маклорена (п.2.2.2.).
Преобразуем рассматриваемую функцию и воспользуемся разложением: 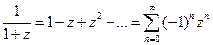 . Имеем:
. Имеем:
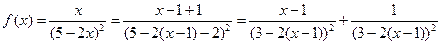 .
.
Разложим сначала в ряд функцию
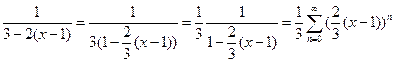 . Область сходимости этого ряда
. Область сходимости этого ряда 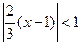 . Степенной ряд в области сходимости можно дифференцировать почленно, поэтому
. Степенной ряд в области сходимости можно дифференцировать почленно, поэтому
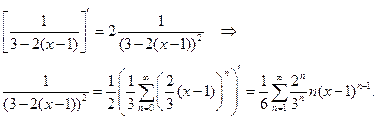
Таким образом, мы получили разложение в ряд для второго слагаемого. Аналогично, для первого слагаемого имеем:
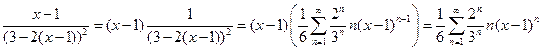 .
.
Складывая эти два ряда, получаем
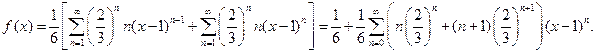
Область сходимости этого ряда 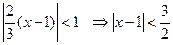 - это круг с центром 1 и радиусом 3/2. Таким образом, радиус сходимости – 3/2.
- это круг с центром 1 и радиусом 3/2. Таким образом, радиус сходимости – 3/2.
Ответ: Степенной ряд имеет вид - 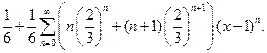
Радиус сходимости - 3/2, область сходимости 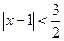 .
.
5. Разложить в ряд Фурье функцию  периода
периода 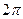 , заданную на отрезке
, заданную на отрезке 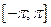 формулой:
формулой: 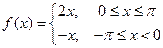 .
.
Решение. Функция  является кусочно-непрерывной, поэтому удовлетворяет условиям Дирихле, значит, эту функцию можно разложить в ряд Фурье, сходящийся к ней в точках непрерывности. Данная функция не является ни четной, ни нечетной, поэтому требуется найти все коэффициенты ряда. Имеем:
является кусочно-непрерывной, поэтому удовлетворяет условиям Дирихле, значит, эту функцию можно разложить в ряд Фурье, сходящийся к ней в точках непрерывности. Данная функция не является ни четной, ни нечетной, поэтому требуется найти все коэффициенты ряда. Имеем: 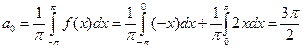 ,
, 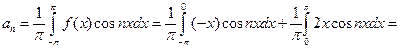
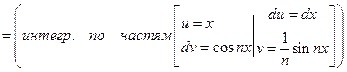 =
= 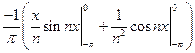 +
+ 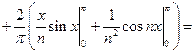
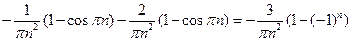 .
.
Аналогично находим 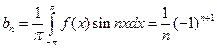 .
.
Исходной функции  соответствует ряд Фурье
соответствует ряд Фурье 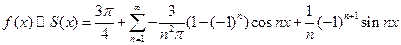 . Функция
. Функция  непрерывна во всех внутренних точках отрезка
непрерывна во всех внутренних точках отрезка  , поэтому, для всех этих точек имеем равенство:
, поэтому, для всех этих точек имеем равенство: 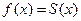 , т.е.
, т.е. 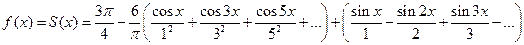 .
.
В точках 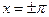 сумма
сумма 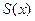 ряда равна
ряда равна 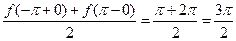 .
.
Графики функций  и
и  показаны на Рис. 11.
показаны на Рис. 11.
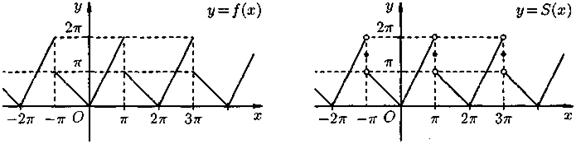
Рис. 11
Ответ. Разложение в ряд Фурье имеет вид: 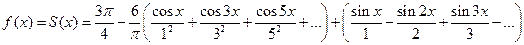 .
.
Варианты заданий контрольной работы № 7
Таблица 1. Варианты задания 1
| № варианта | Пример | № варианта | Пример |
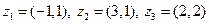
| 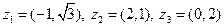
| ||
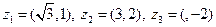
| 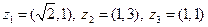
| ||
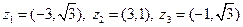
| 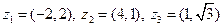
| ||
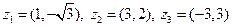
| 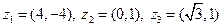
| ||
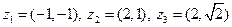
| 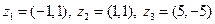
| ||
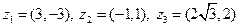
| 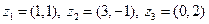
| ||
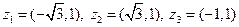
| 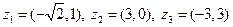
| ||
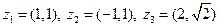
| 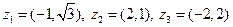
| ||
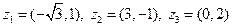
| 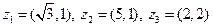
| ||
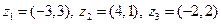
| 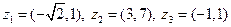
| ||
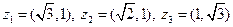
| 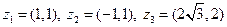
| ||
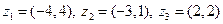
| 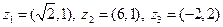
| ||
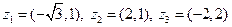
|
Таблица 2. Варианты задания 2
| № варианта | Пример | № варианта | Пример |
а) 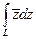 , , 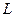 - верхняя полуокружность - верхняя полуокружность 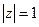 .
б) .
б) 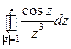
| а) 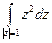 ;
б) ;
б) 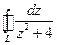 , , 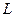 - окружность - окружность 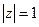
| ||
а) 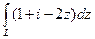 , , 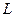 - отрезок прямой между точками - отрезок прямой между точками 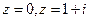 ;
б) ;
б) 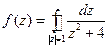
| а) 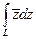 , , 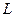 - верхняя полуокружность - верхняя полуокружность 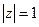 .
б) .
б) 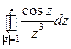
| ||
а) 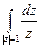 ;
б) ;
б) 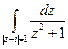
| а) 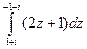 б)
б) 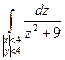
| ||
а) 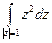 б)
б) 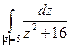
| а) 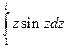 б)
б) 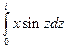
| ||
а) 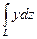 , , 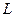 - отрезок прямой между точками - отрезок прямой между точками 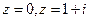 ;
б) ;
б) 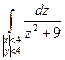
| а) 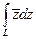 , , 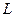 - верхняя полуокружность - верхняя полуокружность 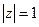 .
б) .
б) 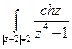
| ||
а) 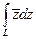 , , 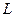 - отрезок прямой между точками - отрезок прямой между точками 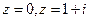 ;
б) ;
б) 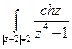
| а) 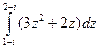 б)
б) 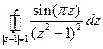
| ||
а) 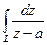 , где , где 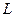 - окружность радиуса - окружность радиуса 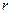 с центром в точке с центром в точке 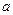 .
б) .
б) 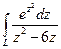 , , 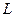 - окружность - окружность 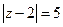
| а) 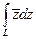 , , 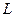 - верхняя полуокружность - верхняя полуокружность 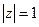 б)
б) 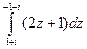
| ||
а) 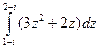 б)
б) 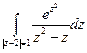
| а) 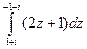 б)
б) 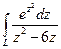 , , 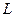 - окружность - окружность 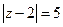
| ||
а) 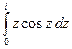 б)
б) 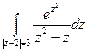
| а) 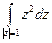 б)
б) 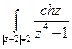
| ||
а) 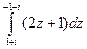 б)
б) 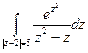
| а) 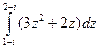 б)
б) 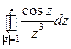
| ||
а) 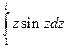 б)
б) 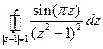
| а) 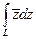 , L – линия, соединяющая точки , L – линия, соединяющая точки 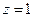 и и 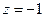 .
б) .
б) 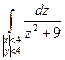
| ||
а) 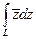 , L – линия, соединяющая точки , L – линия, соединяющая точки 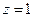 и и 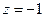 .
б) .
б) 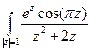
| а) 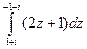 б)
б) 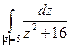
| ||
а) 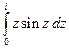 б)
б) 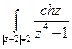
|
Таблица 3. Варианты задания 3
| № варианта | Пример | № варианта | Пример |
а) 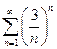 б)
б) 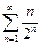
| а) 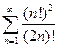 б)
б) 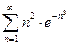
| ||
а) 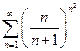 б)
б) 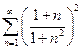
| а) 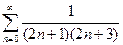 б)
б) 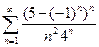
| ||
а) 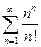 б)
б) 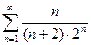
| а) 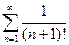 б)
б) 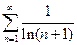
| ||
а) 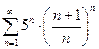 б)
б) 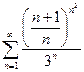
| а) 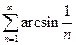 б)
б) 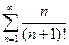
| ||
а) 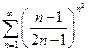 б)
б) 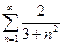
| а) 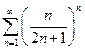 б)
б) 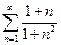
| ||
а) 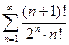 б)
б) 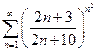
| а) 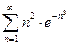 б)
б) 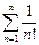
| ||
а) 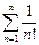 б)
б) 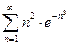
| а) 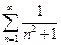 б)
б) 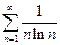
| ||
а) 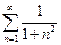 б)
б) 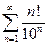
| а) 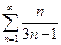 б)
б) 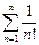
| ||
а) 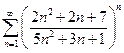 б)
б) 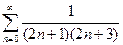
| а) 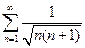 б)
б) 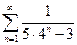
| ||
а) 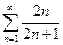 б)
б) 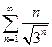
| а) 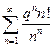 б)
б) 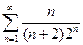
| ||
а) 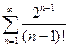 б)
б) 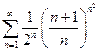
| а) 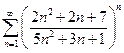 б)
б) 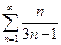
| ||
а) 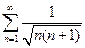 б)
б) 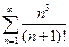
| а) 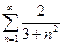 б)
б) 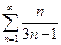
| ||
а) 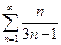 б)
б) 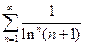
|
Таблица 4. Варианты задания 4
| № варианта | Пример | № варианта | Пример |
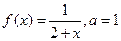
| 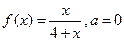
| ||
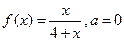
| 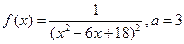
| ||
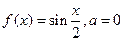
| 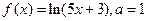
| ||
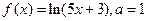
| 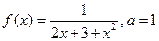
| ||
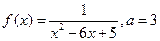
| 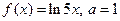
| ||
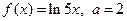
| 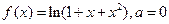
| ||
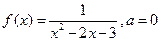
| 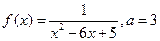
| ||
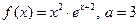
| 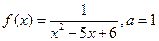
| ||
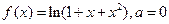
| 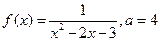
| ||
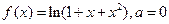
| 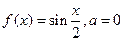
| ||
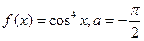
| 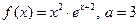
| ||
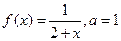
| 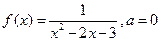
| ||
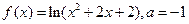
|
Таблица 5. Варианты задания 5
| № варианта | Пример | № варианта | Пример |
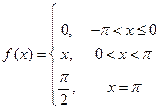
| 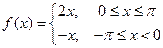
| ||
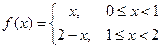
| 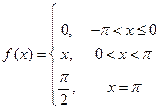
| ||
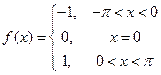
| 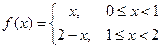
| ||
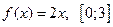
| 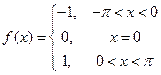
| ||
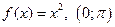
| 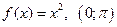
| ||
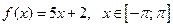
| 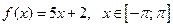
| ||
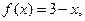 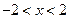
| 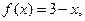 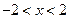
| ||
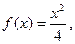 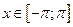
| 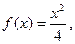 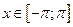
| ||
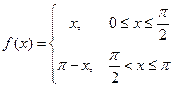
| 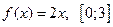
| ||
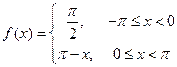
| 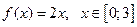
| ||
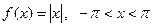
| 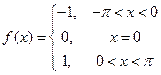
| ||
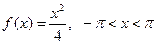
| 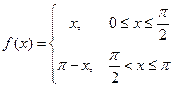
| ||
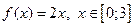
|
 2015-04-01
2015-04-01 581
581








