2015-04-01
2594
А) Константу С находим из свойства нормировки плотности распределения: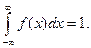 
В данном случае, т.к. плотность содержит переменную под знаком модуля, то интеграл разбивается на два интеграла:
.
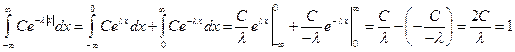Отсюда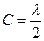 
.
Б) Плотность распределения и функция распределения связаны соотношением: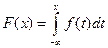 
.
Запишем плотность распределения следующим образом: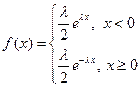 
. Функцию распределения будем искать, используя эти промежутки.
При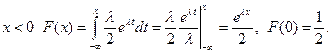 
При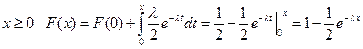 
.
Таким образом, функция распределения имеет вид:
.
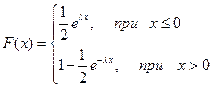В) Математическое ожидание непрерывной случайной величины равно:
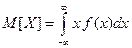. В рассматриваемом случае:
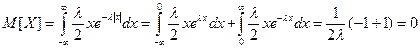(при вычислении интегралов использовалась формула интегрирования по частям).
Дисперсию случайной величины вычислим по формуле: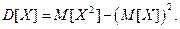 
Так как математическое ожидание равно 0, то дисперсия будет равна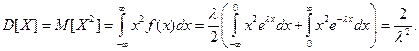 
Ответ: Для непрерывной случайной величины Х: нормировочная константа равна 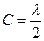, функция распределения 
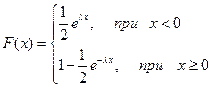, математическое ожидание 
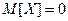, дисперсия 
.
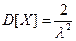4. Задан интервальный вариационный ряд. Рассчитать и построить гистограмму относительных частот по сгруппированным данным, здесь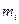 
- частота попадания вариант в промежуток (
).
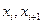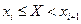| № |  | mi |
| 2 - 4 | 5 | |
| 4 - 6 | 8 | |
| 6 - 8 | 16 | |
| 8 - 10 | 12 | |
| 10 - 12 | 9 |
