| № | Вид | Уравнение прямой |
| Общее уравнение прямой | А x + B y + C = 0 | |
| С угловым коэффициентомk (k = tg a.) | 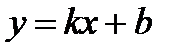
| |
Каноническое (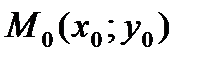 - координаты точки, - координаты точки,
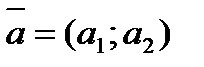 - направляющего вектора) - направляющего вектора)
| 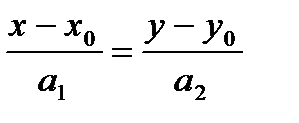
| |
Параметрическое (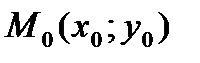 - координаты точки, - координаты точки,
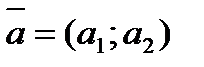 - направляющего вектора) - направляющего вектора)
| 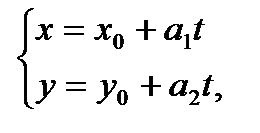
|
Рассмотрим примеры решения типовых задач.
Пример 1. Составьте уравнение прямой, проходящей через точку А (3;-2) и имеющей направляющий вектор 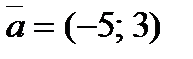 в каноническом и параметрическом виде.
в каноническом и параметрическом виде.
Решение: Определим способ задания прямой: с помощью точки 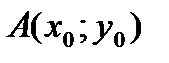
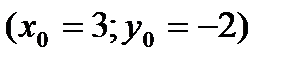 и направляющего вектора
и направляющего вектора 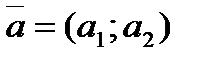
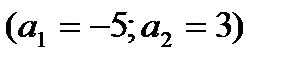 .
.
Подставим координаты точки и направляющего вектора в уравнение 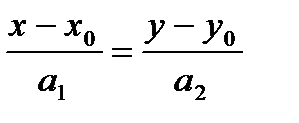 :
: 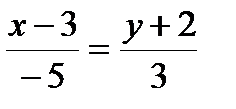 - канонический вид.
- канонический вид.
Подставим координаты точки и направляющего вектора в уравнение 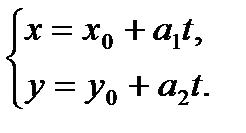 :
: 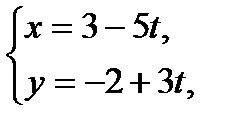 - параметрический вид.
- параметрический вид.
Ответ: 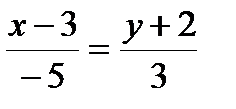 ,
, 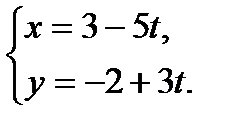
Пример 2. Составьте уравнение прямой, проходящей через точки А (2; 3) и В (7; 5).
Решение: Подставив в формулу 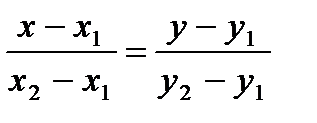 координаты данных точек, получим искомое уравнение прямой:
координаты данных точек, получим искомое уравнение прямой: 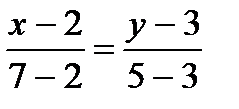 .
.
Ответ: l: 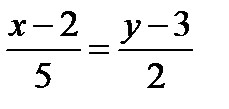 .
.
Пример 3. Составьте уравнение прямой, проходящей через точку M0 (-3; 2) и образующей с положительным направлением оси ОХ угол 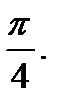
Решение: Найдём угловой коэффициент прямой: k = tg a. 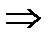 k = tg
k = tg 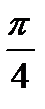 ; k = 1.
; k = 1.
Подставим k и координаты точки M0 в уравнение 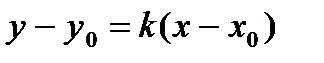 :
:
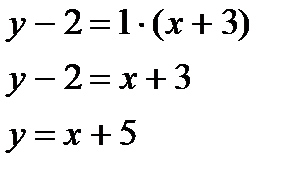 Ответ:
Ответ: 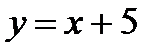
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 3, §3.4, стр. 61 – 63.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 4, §19 – 21, стр. 122 – 132.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 3, §5, стр. 141 - 149.
 2015-04-01
2015-04-01 470
470








