Б) Последовательное соединение емкости и активного сопротивления

Реальный конденсатор имеет активное и емкостное сопротивле­ния.

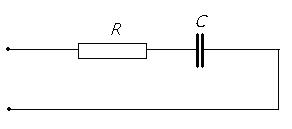
Рис.41.4. Электрическая цепь реального конденсатора

Построим векторную диаграмму и гра­фики для этого случая.

На рис.41.5 вектор I обозначает переменный ток катушки.

Часть напряжения сети, падающая в сопротивлении R изображена век­тором U_R, совпадающим по фазе с током. Напряжение на ёмкости показано вектором U_С, который отстает от тока на угол 90^о.

Напряжение сети U должно быть равно геометрической сумме активного U_{R t} и емкостного U_С падений напряжения. Для получения геометрической суммы необхо­димо на векторах U_R и U_С построить параллелограмм. Его диа­гональ (равнодействующая) даст напряжение сети U.

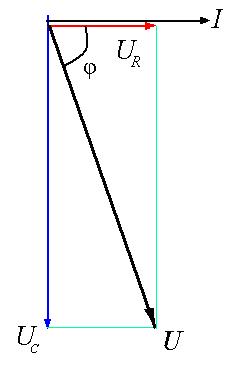
Рис.41.5. Векторная диаграмма для цепи с последовательным соединением R и С.

Ток в цепи с последовательно соединенными активным сопротивлением и емкостью будет иметь одно и то же значение. Поэтому, разделив величины векторов напряжений на одно и то же значение тока, мы получим значения сопротивлений цепи. Они образуют треугольник сопротивлений

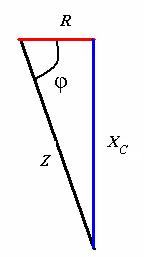Рис.41.6. Треугольник сопротивлений

Из треугольника сопротивлений следует, что

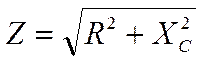
Где: Z - полное сопротивление цепи (Ом)

R - активное сопротивление цепи (Ом)

X_С - емкостное сопротивление цепи (Ом)