Оценка статистической значимости регрессии

Рассмотрим вопрос о том, как отличить «хорошие» оценки МНК от «плохих». При этом, конечно, предполагается что существуют критерии качества рассчитанной линии регрессии.

Перечислим способы, которые помогают решить вопрос о достоинствах рассчитанной линии регрессии:

· построение доверительных интервалов и оценка статистической значимости коэффициентов регрессии по 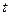-критерию Стьюдента;

· дисперсионный анализ и 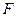- критерий Фишера;

· проверка существенности выборочного коэффициента корреляции (детерминации).

Перейдем к подробному изложению свойств оценок и способов

проверки их значимости.

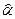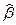Можно показать, что оценки и полученные МНК по (2.8) с учётом ограничений (2.3)-(2.5) являются линейными несмещенными оценками и обладают наименьшими дисперсиями (являются эффективными) в классе линейных несмещённых оценок (теорема Гаусса-Маркова).

Для вычисления интервальных оценок 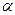и 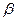предполагают нормальное распределение случайной величины и. Для получения интервальных оценок 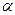и 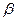оценим дисперсию случайного члена 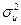по отклонениям 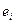. В качестве оценки дисперсии ошибки 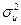возьмем величину:

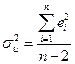(2.12)

Вычислим величину

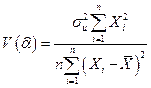
и 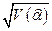- стандартную ошибку коэффициента регрессии 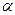. Статистика

,

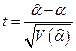имеет 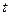-распределение Стьюдента. Так как 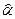является несмещенной оценкой, то для заданного 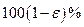уровня значимости доверительный интервал для 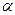имеет вид:

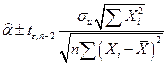или 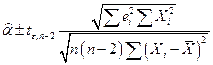, (2.13)

где 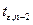- табличное значение 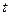распределения с 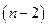степенями свободы на уровне значимости .

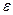Рассмотрим величину

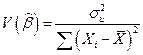
и 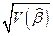стандартную ошибку коэффициента регрессии .

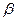Замечание. Стандартная ошибка дает только общую оценку степени точности коэффициента регрессии. Очевидно, что, чем больше будет величина дисперсии случайного члена (и соответственно ее оценка - выборочная дисперсия остатков), тем существеннее величина стандартной ошибки, и с большей вероятностью можно говорить о том, что полученная оценка неточна.

Статистика

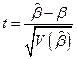
имеет 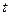-распределение Стьюдента. Так как 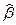является несмещенной оценкой, то для заданного 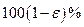уровня значимости доверительный интервал для 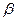имеет вид

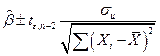или 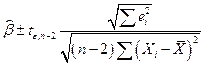(2.14)

где 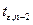- табличное значение 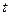распределения с 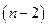степенями свободы на уровне значимости .

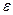Проверим гипотезу о равенстве нулю коэффициента 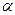, т.е.

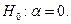
С учетом статистики 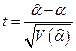для 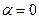, учитывая формулу для 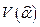, получим

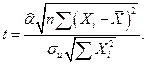(2.15)

Если вычисленное по (2.15) значение 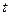будет больше 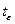для заданного критического уровня значимости 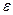, то гипотеза 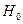о равенстве нулю коэффициента 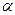отклоняется, если же 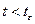, то гипотеза 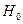принимается.

Аналогично для проверки гипотезы о равенстве нулю коэффициента 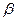, т.е.

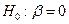
рассчитаем статистику

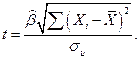(2.16)

Если вычисленное по (2.16) значение 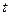будет больше 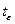для заданного критического уровня значимости 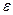, то гипотеза 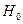о равенстве нулю коэффициента 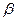отклоняется, если же 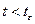, то гипотеза 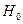принимается.

Заметим, что формулу (2.12) можно упростить и записать в виде:

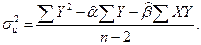(2.17)

Пример. Приведем расчеты для примера в табл. 2.1. По формуле (2.17) рассчитаем дисперсию ошибки:

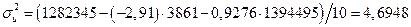или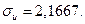

Найдем доверительный интервал для а по первой из формул (2.13):

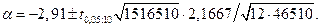
По таблице -распределения находим:

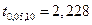и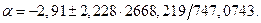

Откуда 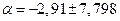или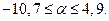

С вероятностью 0,95 истинные значения а находятся в интервале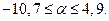

Аналогично найдем доверительный интервал для 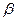по первой из формул (2.14): 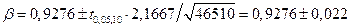и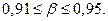

Кроме того по экономическому смыслу переменных примера следует ожидать, что 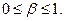Поскольку доверительный интервал не включает 0 и 1, то результаты регрессии соответствуют гипотезе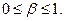

Проверим гипотезу о равенстве нулю коэффициента 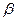, т.е. 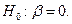Рассчитаем 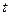-статистику по формуле (2.16):

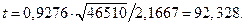
Табличное значение 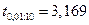, так как 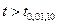, то гипотеза о том, что 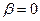отклоняется. Можно говорить о том, что коэффициент 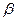значимо отличен от нуля.

Разложим общую вариацию значений 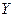около их выборочного среднего 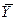на составляющие (см. рис. 2.1):

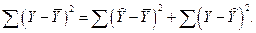
Сумма квадратов отклонений от среднего в выборке равна сумме квадратов отклонений значений 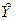, полученных по уравнению регрессии, от выборочного среднего 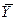плюс сумма квадратов отклонений 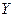от линии регрессии .

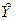Первую связывают с линейным воздействием изменений переменной 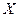и называют объясненной.

Вторая составляющая является остатком и называется необъясненной долей вариации переменной У.

Следует отметить, что долю дисперсии, объясняемую регрессией, в общей дисперсии результативной переменной 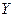характеризует коэффициент детерминации, определяемый по формуле (2.10), которая может быть преобразована с учетом (2.18) к виду:

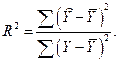
Про верим гипотезу об отсутствии линейной Функциональной связи между 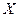и 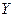, т.е. гипотезу 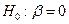. Другими словами, оценим значимость уравнения регрессии (2.6) в целом. Для проверки гипотезы сведем необходимые вычисления в таблицу (табл.2.3).

Соотношение

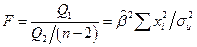(2.19)

удовлетворяет 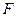- распределению Фишера с 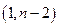степенями свободы. Критические значения этой статистики 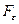для уровня значимости 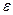затабулированы.

Если 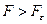, то гипотеза об отсутствии связи между переменным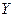и и 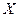отклоняется, в противном случае гипотеза 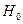принимается и уравнение регрессии незначимо.

Источник вариации	Сумма квадратов отклонений	Число степе- ней свободы	Среднее квадратов отклонений
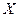
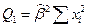
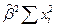
Остаток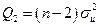
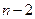
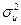
Общая вариация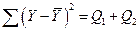

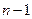
Таблица дисперсионного анализа

Пример. Для примера табл. 2.1, с учетом предыдущих вычислений, получаем таблицу анализа дисперсии - табл. 2.4.

Источник вариации	Сумма квадратов отклонений	Число степеней свободы	Среднее квадратов отклонений
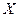
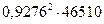
			40019б1
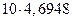
			4б7
			-

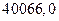
Таблица 2.4. Таблица анализа дисперсии (пример в табл.2.1)

Применяя формулу (2.19), получим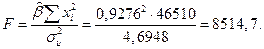

Табличное значение 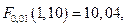так что имеющиеся данные позволяют отвергнуть гипотезу об отсутствии связи между личными доходами и индивидуальным потреблением.