Будем предполагать в рамках модели (2.2) линейную зависимость между двумя переменными 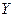 и Х, т.е. имеем модель парной регрессии в виде:
и Х, т.е. имеем модель парной регрессии в виде:
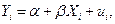
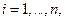
при условии выполнения основных предпосылок регрессионного анализа
а. 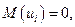
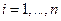 .
.
б. 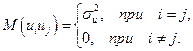
в. 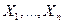 - неслучайные величины.
- неслучайные величины.
Предположим, что имеется выборка значений 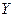 и
и 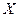 .
.
Обозначим арифметические средние (выборочные математические ожидания) для переменных 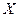 и
и 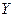 :
:
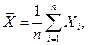
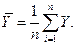
Запишем уравнение оцениваемой линии в виде:
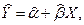
где 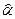 и
и 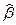 - оценки неизвестных параметров
- оценки неизвестных параметров 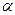 и
и 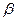 , а
, а 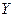 - ордината этой линии.
- ордината этой линии.
Пусть 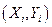 одна из пар наблюдений. Тогда отклонение этой точки (см. рис. 2.1) от оцениваемой линии будет равно
одна из пар наблюдений. Тогда отклонение этой точки (см. рис. 2.1) от оцениваемой линии будет равно 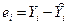 .
.
Принцип метода наименьших квадратов (МИК) заключается в выборе таких оценок 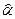 и
и 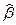 , для которых сумма квадратов отклонений для всех точек является минимальной.
, для которых сумма квадратов отклонений для всех точек является минимальной.
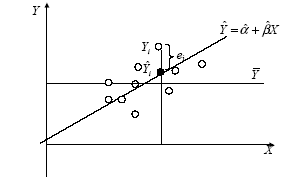
Рис. 2.1. Иллюстрация принципа МНК
Необходимым условием для этого служит обращение в нуль частных производных функционала:
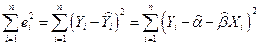
по каждому из параметров. Имеем
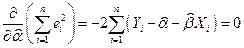 ;
; 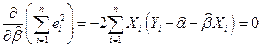 .
.
Упрощая последние равенства, получим стандартную форму нормальных уравнений, решение которых даёт искомые оценки параметров:
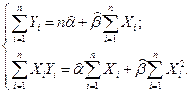 (2.7)
(2.7)
Из (2.7) получаем:
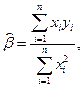
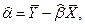 (2.8)
(2.8)
где 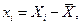
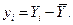
Пример. Для иллюстрации вычислений при отыскании зависимости с помощью метода наименьших квадратов рассмотрим пример (табл. 2.1).
| Год | Индивидуальное потребление, млрд. долл. | Личные доходы, млрд. долл. |
Таблица 2.1 Индивидуальное потребление и личные доходы (США, 1954-1965 гг.)
| Год | 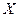
| 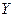
| 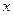
| 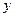
| 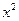
| 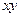
| 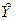
| 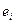
|
| -93 | -85,75 | 7974,75 | 235,48 | 0,52 | ||||
| -75 | -67,75 | 5081,25 | 252,18 | 1,82 | ||||
| -57 | -54,75 | 3120,75 | 268,88 | -1,88 | ||||
| -41 | -40,75 | 1670,75 | 283,72 | -2,72 | ||||
| -31 | -31,75 | 984,25 | 292,99 | -2,99 | ||||
| -13 | -10,75 | 139,75 | 309,69 | 1,31 | ||||
| 3,25 | 321,75 | 3,25 | ||||||
| 13,25 | 185,5 | 334,74 | 0,26 | |||||
| 33,25 | 1163,75 | 354,22 | 0,78 | |||||
| 53,25 | 2928,75 | 372,77 | 2,23 | |||||
| 79,25 | 6894,75 | 402,45 | -1,45 | |||||
| 109,25 | 13000,75 | 432,13 | -1,13 | |||||
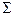
| 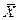 =350,00 =350,00
| 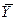 =321,75 =321,75
| 0,00 | 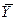 =321,75 =321,75
| 0,00 |
Рабочая таблица расчетов (по данным табл. 2.1)
Заметим, что исходные данные должны быть выражены величинами примерно одного порядка. Вычисления удобно организовать, как показано в таблице 2.2. Сначала рассчитываются 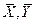 ,затем
,затем 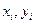 . Результаты заносятся в столбцы 3 и 4. Далее определяются
. Результаты заносятся в столбцы 3 и 4. Далее определяются 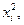
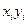 и заносятся в 5 и 6 столбцы таблицы 2.2. По формулам (2.8) получим искомые значения параметров
и заносятся в 5 и 6 столбцы таблицы 2.2. По формулам (2.8) получим искомые значения параметров
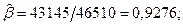
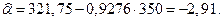
Оцененное уравнение регрессии запишется в виде 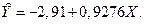
Полученное уравнение можно использовать длярасчёта точечного прогноза, в том числе и на перспективу. Подставляя последовательно значения Х из второго столбца табл. 2.2 в уравнение 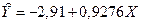 , получим предпоследний столбец табл. 2.2 для прогнозных значений
, получим предпоследний столбец табл. 2.2 для прогнозных значений 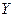 . Ошибка прогноза вычисляется по формуле
. Ошибка прогноза вычисляется по формуле 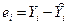 и дана в последнем столбце рабочей таблицы
и дана в последнем столбце рабочей таблицы
Заметим, что ошибка прогноза 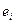 фактически является оценкой значений
фактически является оценкой значений 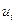 . График ошибки
. График ошибки 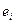 представлен на рис. 2.2. Отметим факт равенства нулю суммы
представлен на рис. 2.2. Отметим факт равенства нулю суммы 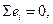 что согласуется с первым ограничением модели парной регрессии -
что согласуется с первым ограничением модели парной регрессии - 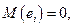
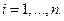
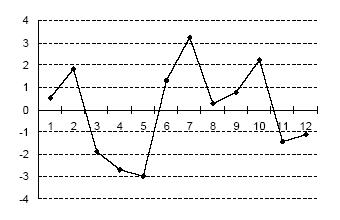
Рис. 2.2 График ошибки прогноза
 2015-04-01
2015-04-01 397
397








