2015-04-01
587
Запишем структурные уравнения в общем виде:
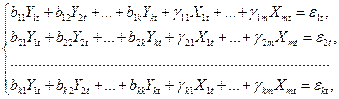(6.17)
где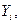 
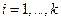– эндогенные переменные;
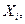
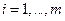– экзогенные переменные или лагированные значения эндогенных переменных (предопределенные переменные);
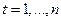– номер наблюдения;
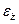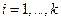, – случайные ошибки.
Будем считать, что в каждом уравнении один из коэффициентов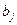 
при какой-либо эндогенной переменной равен единице (условие нормировки, позволяющее разрешить систему (6.17) относительно эндогенных переменных).
Обозначим:
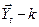-вектор эндогенных переменных,
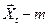-вектор эндогенных переменных,
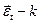-вектор ошибок измерения,
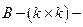матрица коэффициентов 
,
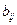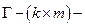матрица коэффициентов 
.
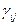Тогда СФМ (6.17) в матричной форме имеет вид:
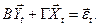(6.18)
Будем считать, что
- экзогенные переменные
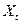не коррелированы с ошибками 
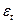, - математическое ожидание 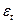равно нулю,
- ковариационная матрица ошибок
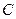известна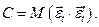 
- Матрица 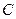не зависит от времени и положительно определена,
- при
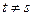векторы 
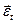и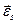 
некоррелированы, - матрица
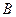невырождена.
Перейдем от СФМ (6.18) к ПФМ, для чего запишем решение уравнения (6.18):
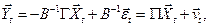(6.19)
где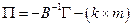 
-матрица коэффициентов ПФМ,
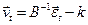– k -вектор ошибок ПФМ.
Если эндогенные переменные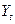 
и ошибки 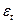в СФМ коррелированы, обычный МНК дает смещенные и несостоятельные оценки структурных коэффициентов (элементов матриц 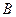и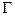 
). Коэффициенты ПФМ (6.19) могут быть оценены состоятельно, т. к. переменные 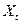не коррелированы со структурными ошибками 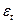и, следовательно, с ошибками ПФМ 
.
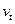Структурные коэффициенты 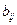и и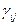дентифицируемы, если они могут быть вычислены через коэффициенты матрицы 
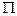ПФМ (6.19). Уравнение в СФМ (6.18) называется идентифицируемым, если идентифицируемы все его коэффициенты.
ПФМ (6.19) позволяет состоятельно оценить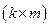 
элементов матрицы 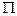. В то же время в СФМ (6.18) неизвестными являются 
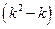− элементов матрицы 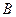(минус k с учетом условия нормировки) и 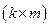элементов матрицы 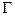. Таким образом, превышение числа неизвестных структурных коэффициентов над числом известных коэффициентов ПФМ равно 
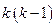и, следовательно, в общем случае СФМ (6.18) неидентифицируема. Однако реально часть структурных коэффициентов равна нулю, что позволяет решить задачу идентификации.
