2015-04-01
839
В таких системах уравнения связаны лишь благодаря наличию корреляции между ошибками в разных уравнениях. Например, зависимости инвестиций компаний «Газпром» и «Лукойл» от дохода и размера основного фонда имеют коррелированные ошибки (поскольку оба предприятия в данный период времени действуют в одной и той же экономической среде), что делает эти зависимости связанными.
Можно оценивать внешне несвязанные уравнения по отдельности. Однако эффективность оценивания можно повысить, если объединить уравнения в одно и применить к нему обобщенный МНК.
В качестве примера рассмотрим систему двух уравнений:
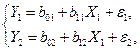(6.7)
где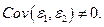 
Обозначим
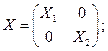
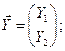
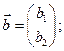
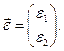
Тогда уравнения (6.7) можно объединить в одно векторно-матричное:
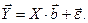(6.8)
Пусть
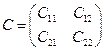
-ковариационная матрица ошибок регрессии уравнения (6.8):
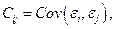
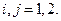
Тогда оценка вектора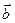 
с использованием обобщенного МНК находится по формуле:
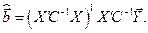
Для практического применения этого способа следует оценить ковариационную матрицу ошибок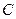 
. Это можно сделать, применив обычный МНК к уравнениям системы (6.7) по отдельности, определив остатки регрессии и приняв в качестве оценок 
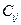выборочные коэффициенты ковариации:
|
|
|
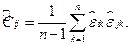
Пример. Идентификация внешне несвязанных уравнений обобщенным МНК.
Идентифицировалась модель
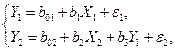(6.9)
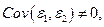
где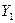 
– стоимость полуфабриката,
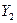– цена конечной продукции,
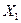– сумма цен на сырье,
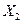– обобщенный фактор конечного производства,
ПФМ модели (6.9):
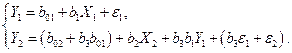(6.10)
Оценка модели (6.9) при раздельном оценивании уравнений:
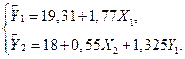(6.11)
Оценка модели (6.10) обобщенным МНК:
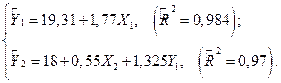
Возвращаясь от ПФМ к СФМ (6.9), получаем
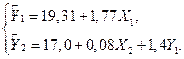(6.12)
Модель (6.12) является более точной по сравнению с моделью (6.11). При этом коэффициент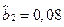 
оказался незначимым.
