Алгебры разного типа, очевидно, имеют существенно различное строение. Если же алгебры имеют одинаковый тип, то наличие у них сходства характеризуется с помощью вводимых ниже понятий гомоморфизма и изоморфизма.
Пусть даны две алгебры
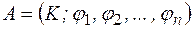 и
и 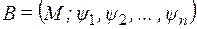
одинакового типа, т. е. арности 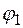 и
и 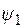 ;
; 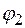 и
и 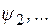 ;
; 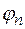 и
и 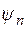 – одинаковы.
– одинаковы.
Гомоморфизмом алгебры А в алгебру В называется отображение – 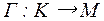 , удовлетворяющее условию:
, удовлетворяющее условию:
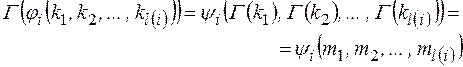 (1)
(1)
для всех 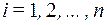 (
(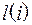 – арность операций
– арность операций 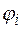 и
и 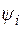 .
.
Смысл условия (1):
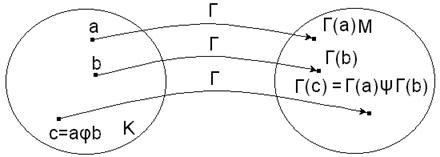
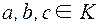
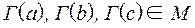
независимо от того, выполнена ли сначала операция 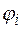 в множестве K и затем произведено отображение Г, либо сначала произведено отображение Г, а затем в множестве M выполнена соответствующая операция
в множестве K и затем произведено отображение Г, либо сначала произведено отображение Г, а затем в множестве M выполнена соответствующая операция 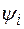 , результат будет одинаков.
, результат будет одинаков.
Изоморфизмом алгебры А на алгебру В называется взаимно однозначный гомоморфизм. В этом случае существует обратное отображение 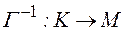 , так же взаимно однозначное.
, так же взаимно однозначное.
Пусть 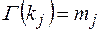 ,
, 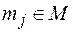 . Тогда
. Тогда 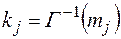 . Заменим в (1) левые части этих равенств на правые и применим
. Заменим в (1) левые части этих равенств на правые и применим 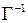 к обеим частям получившегося равенства. Так как
к обеим частям получившегося равенства. Так как 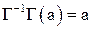 , то получим:
, то получим:
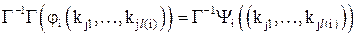 ,
,
учитывая, что 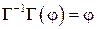 ,
,
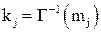 ,
, 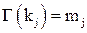 , получим
, получим
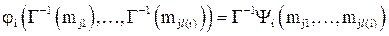 . (2)
. (2)
Равенство (2) – это то же равенство (1) с заменой Г на 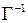 , элементов множества K на элементы множества М и переменой местами
, элементов множества K на элементы множества М и переменой местами 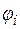 и
и 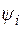 . Иначе говоря,
. Иначе говоря, 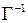 – это изоморфизм В на А.
– это изоморфизм В на А.
Утверждение 1:
Если существует изоморфизм А на В, то существует изоморфизм В на А; при этом алгебры А и В называются изоморфными.
Утверждение 2:
Мощности несущих множеств изоморфных алгебр равны (при гомоморфизме это равенство может не выполняться).
Автоморфизм на себя или автоморфизм – это гомоморфизм при условии, что А = В.
Изоморфизм в себя – изоморфизм 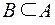 .
.
Примеры:
1. Пусть 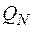 – множество всех целых чисел;
– множество всех целых чисел; 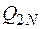 – множество всех четных чисел;
– множество всех четных чисел;
а) алгебры 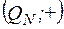 и
и 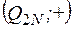 изоморфны. Изоморфизмом является отображение
изоморфны. Изоморфизмом является отображение 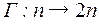 , причем, условие (1) здесь имеет вид: 2 (a + b) = 2 a + 2 b. Поскольку
, причем, условие (1) здесь имеет вид: 2 (a + b) = 2 a + 2 b. Поскольку 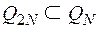 , то Г – изоморфизм алгебры
, то Г – изоморфизм алгебры 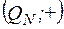 в себя.
в себя.
б) отображение 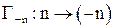 является для алгебры
является для алгебры 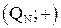 автоморфизмом.
автоморфизмом.
Условие (1) имеет вид:
- (a + b) = (-a) + (-b);
в) отображение 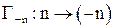 для алгебры
для алгебры 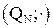 не является автоморфизмом, так как
не является автоморфизмом, так как
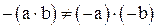 .
.
2. Изоморфизмом между алгебрами 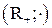 и
и 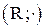 является отображение
является отображение 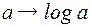 (
(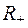 – положительное подмножество R).
– положительное подмножество R).
Условие (1) имеет вид равенства:
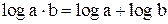 .
.
3. Булевы алгебры Кантора 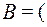 B(U),
B(U), 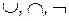 ) и
) и 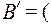 B(
B(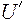 ),
), 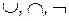 ), образованные двумя различными множествами U и
), образованные двумя различными множествами U и 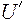 одинаковой мощности, изоморфны. Операции у них просто одинаковы, а отображением Г может служить любое взаимно однозначное соответствие между U и
одинаковой мощности, изоморфны. Операции у них просто одинаковы, а отображением Г может служить любое взаимно однозначное соответствие между U и 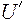 .
.
Утверждение 3:
Отношение изоморфизма является отношением эквивалентности на множестве алгебр:
– рефлексивность отношения изоморфизма очевидна;
– симметричность следует из существования обратного изоморфизма;
– транзитивность устанавливается следующим образом: если 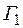 – изоморфизм А на В,
– изоморфизм А на В, 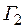 – изоморфизм В на С, то изоморфизмом А на С будет композиция
– изоморфизм В на С, то изоморфизмом А на С будет композиция 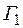 и
и 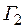 .
.
Классами эквивалентности в разбиении по отношению изоморфизма являются классы изоморфных между собой алгебр. Понятие изоморфизма – одно из важнейших в математике. Его сущность, как видно из примеров можно выразить так: если алгебры А и В изоморфны, то элементы и операции в В можно переименовать так, что В совпадет с А.
Из условия (1) изоморфизма следует, что любое эквивалентное соотношение в алгебре А сохраняется в любой изоморфной ей алгебре 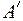 . Это позволяет получить такие соотношения в алгебре А и автоматически распространить их на все алгебры, изоморфные А. Распространенное в математике выражение «рассматривать с точностью до изоморфизма» означает, что рассматриваются только те свойства объектов, которые сохраняются при изоморфизме, т. е. являются общими для всех изоморфных объектов.
. Это позволяет получить такие соотношения в алгебре А и автоматически распространить их на все алгебры, изоморфные А. Распространенное в математике выражение «рассматривать с точностью до изоморфизма» означает, что рассматриваются только те свойства объектов, которые сохраняются при изоморфизме, т. е. являются общими для всех изоморфных объектов.
В частности, изоморфизм сохраняет ассоциативность, коммутативность, дистрибутивность.
 2015-04-01
2015-04-01 7381
7381








