1. Проверить коммутативность и ассоциативность операций.
1) сложение чисел; 2) умножение чисел; 3) сложение матриц; 4) умножение матриц (проверить на примере квадратных матриц А, В и С 2-ого порядка); 5) возведение в степень; 6) ln xy (где х, у >0); 7) х-у; з) х/у.
2.Проверить дистрибутивность слева и справа операции ψ отношению к операции φ.
1) φ – сложение чисел, ψ – умножение чисел; 2) φ – умножение чисел, ψ – сложение чисел; 3) φ – объединение множеств, ψ – пересечение множеств; 4) φ – пересечение множеств, ψ – объединение множеств; 5) φ – умножение чисел, ψ – возведение в степень; 6) φ – возведение в степень, ψ – умножение чисел; 7) φ – возведение в степень, ψ – сложение чисел.
3. На множестве 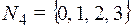 задать с помощью таблицы Келли операции
задать с помощью таблицы Келли операции 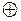 – сложение по модулю 4 и
– сложение по модулю 4 и 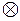 – умножение по модулю 4. Продемонстрировать на примере их коммутативность, ассоциативность, дистрибутивность
– умножение по модулю 4. Продемонстрировать на примере их коммутативность, ассоциативность, дистрибутивность 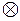 по отношению к
по отношению к 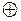 , отсутствие дистрибутивности
, отсутствие дистрибутивности 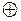 по отношению к
по отношению к 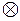 .
.
4. На множестве 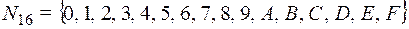 задать с помощью таблицы Келли операции
задать с помощью таблицы Келли операции 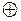 – сложение по модулю 16 и
– сложение по модулю 16 и 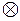 – умножение по модулю 16.
– умножение по модулю 16.
Найти значения выражений:
1) 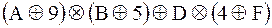 ;
;
2) 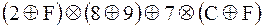 .
.
5. В конечной алгебре поля 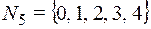 рассчитать значения выражений:
рассчитать значения выражений:
1) 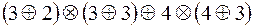 ;
;
2) 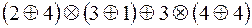 .
.
6. В поле 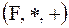 , операции которого заданы таблицами Келли
, операции которого заданы таблицами Келли
| * | a | b | c | d | + | a | b | c | d | |
| a | a | a | a | a | a | a | b | c | d | |
| b | a | b | c | d | b | b | a | d | c | |
| c | a | c | d | b | c | c | d | a | b | |
| d | a | d | b | c | d | d | c | b | а |
1) единичный элемент по операции *;
2) единичный элемент по операции +;
3) противоположный и обратный элемент для каждого элемента 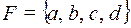 ;
;
4) найти значения выражений:
а) 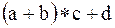 ;
;
б) 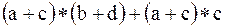 ;
;
в) 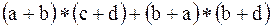 .
.
5) решить систему
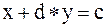 ;
;
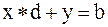 .
.
7. Дано множество 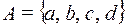 . Задано поле
. Задано поле 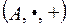 , где
, где
 | a | b | c | d | + | a | b | c | d | |
| a | a | a | a | a | a | a | b | c | d | |
| b | a | b | c | d | b | b | a | d | c | |
| c | a | c | d | b | c | c | d | a | b | |
| d | a | d | b | c | d | d | c | b | а |
Найти единичные элементы по операциям 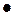 и +, противоположные элементы для каждого, решить систему:
и +, противоположные элементы для каждого, решить систему:
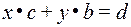 ;
;
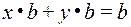 .
.
8. Доказать единственность единичного элемента в группе.
9. Доказать единственность обратного элемента в группе.
10. Пусть 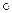 ассоциативная операция, заданная на множестве А, такая что для каждого элемента
ассоциативная операция, заданная на множестве А, такая что для каждого элемента 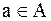 существует обратный элемент
существует обратный элемент 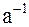 . Доказать, что
. Доказать, что 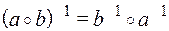 .
.
11. Дано 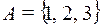 . На множестве А заданы преобразования
. На множестве А заданы преобразования 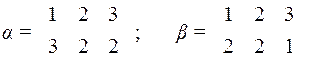 . На множестве преобразований
. На множестве преобразований 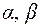 задана операция композиции преобразований
задана операция композиции преобразований 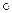 .
.
Проверить, будет ли алгебра 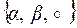 полугруппой.
полугруппой.
12. Составить полугруппу с операцией 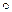 – композиция преобразований, для которой множество подстановок
– композиция преобразований, для которой множество подстановок 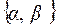 является системой образующих.
является системой образующих.
Что надо сделать, чтобы эта полугруппа стала моноидом.
13. Пусть S – множество всех перестановок 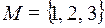 . Определить свойства алгебры
. Определить свойства алгебры 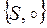 . Будет ли оно группой? Будет ли группа абелевой?
. Будет ли оно группой? Будет ли группа абелевой?
14. Будет ли алгебра (B(U), 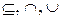 ) решеткой? Изобразить диаграмму Хасса.
) решеткой? Изобразить диаграмму Хасса.
15. Будет ли алгебра (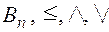 ) решеткой? Изобразить диаграмму Хасса.
) решеткой? Изобразить диаграмму Хасса.
16. Является ли решеткой множество целых чисел Z с операциями 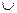 и
и  , таких что для любых
, таких что для любых 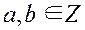 выполняется:
выполняется:
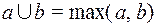 ,
, 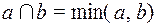 .
.
17. Будет ли решеткой множество, диаграмма Хасса которой изображена на рисунке. Почему?
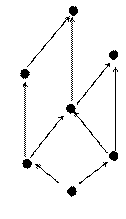
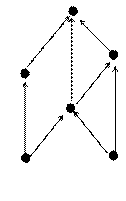
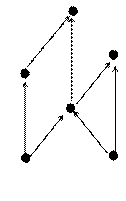
Рис. 1 Рис. 2 Рис. 3
18. Проверить на примере выполнение условия изоморфизма между алгебрами:
1) (B(U), 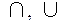 , ┐) и (
, ┐) и (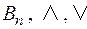 , ┐);
, ┐);
2) (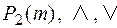 , ┐); (B (U),
, ┐); (B (U), 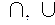 , ┐), где
, ┐), где 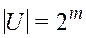 .
.
19. Определить изоморфны ли алгебры:
1) 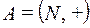 и
и 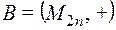 , где гомоморфизм задается
, где гомоморфизм задается 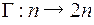 ;
;
2) 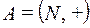 и
и 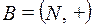 , где гомоморфизм задается
, где гомоморфизм задается 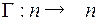 ;
;
3) 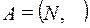 и
и 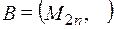 , где гомоморфизм задается
, где гомоморфизм задается 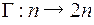 ;
;
4) 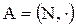 и
и 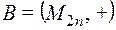 , где гомоморфизм задается
, где гомоморфизм задается 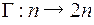 ;
;
5) 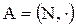 и
и 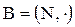 , где гомоморфизм задается
, где гомоморфизм задается 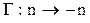 ;
;
6) 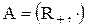 и
и 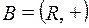 , где гомоморфизм задается
, где гомоморфизм задается 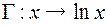 ;
;
7) 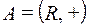 и
и 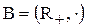 , где гомоморфизм задается
, где гомоморфизм задается 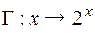 ;
;
 2015-04-01
2015-04-01 3897
3897