Пусть интерпретация 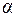 определена на всех высказывательных переменных, встречающихся в формулах множества
определена на всех высказывательных переменных, встречающихся в формулах множества 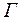 . Говорят, что
. Говорят, что 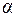 выполняет
выполняет 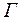 или
или 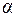 модель
модель 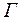 , если каждая формула
, если каждая формула 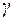 из
из 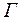 принимает значение «истина», при интерпретации
принимает значение «истина», при интерпретации 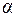 . Говорят, что
. Говорят, что 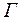 выполнимо, если
выполнимо, если 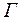 имеет модель. Если
имеет модель. Если 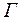 не выполнимо, то пишут
не выполнимо, то пишут 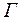 ÷=.
÷=.
Пусть 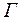 – множество формул логики высказываний, А – произвольная формула. Говорят, что множество
– множество формул логики высказываний, А – произвольная формула. Говорят, что множество 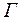 логически влечет формулу А, если любая модель
логически влечет формулу А, если любая модель 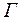 являются моделью для А и обозначается
являются моделью для А и обозначается 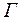 ÷= А.
÷= А.
Утверждение того, что некоторое высказывание (заключение) следует из других высказываний (посылок), называется аргументом. Аргумент часто представляют в виде:
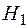
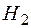
... гипотезы
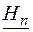
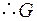 заключение
заключение
Аргумент называется правильным, если из множества гипотез логически следует заключение аргумента.
Второе правило исчисления высказываний: Modus Ponens.
Правило Modus Ponens: 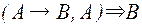 , т.е.
, т.е.
«Если 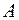 , то
, то 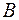 ; но
; но 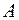 истинно, следовательно, истинно
истинно, следовательно, истинно 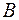 ».
».
 2015-04-01
2015-04-01 391
391








