Решение логарифмических неравенств основано на свойствах монотонности логарифмической функции.
Перечислим некоторые методы решения логарифмических неравенств.
1. При 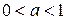 неравенства вида
неравенства вида
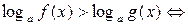
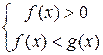 .
.
При 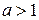
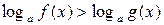
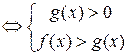 .
.
2. Замена переменной.
Пример 7.19. Решить неравенство 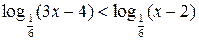 .
.
Решение. Так как основание логарифмов 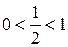 , то исходное неравенство равносильно системе:
, то исходное неравенство равносильно системе:
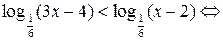
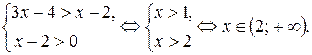
Ответ: 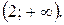
Пример 7.20. Решить неравенство 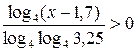 .
.
Решение. Заметим, что
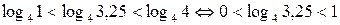 ,
,
тогда
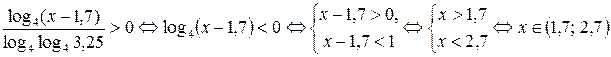 .
.
Ответ: 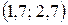 .
.
Пример 7.21. Решить неравенство 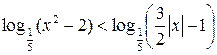 .
.
Решение. Так как 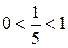 , то
, то
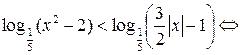
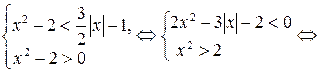
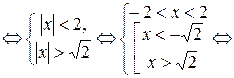
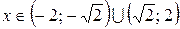 .
.
Ответ: 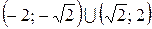 .
.
Пример 7.22. Решить неравенство 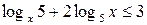 .
.
Решение. Область определения данного неравенства: 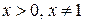 .
.
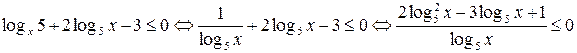 .
.
Сделаем замену: 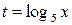 , тогда
, тогда
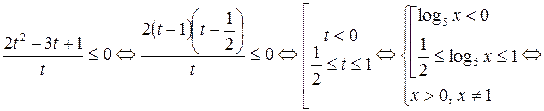
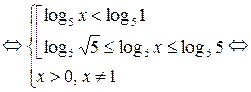
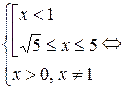
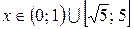 .
.
Ответ: 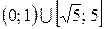 .
.
Пример 7.23. Решить неравенство 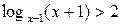 .
.
Решение. Рассмотрим два случая.
1. Если 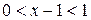 , то
, то
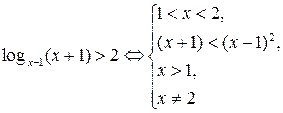
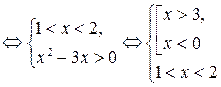 ,
,
нет решений.
2. Если 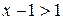 , то
, то
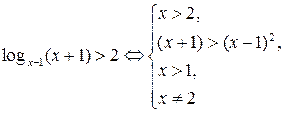
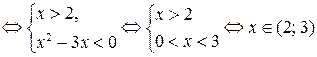 .
.
Ответ: 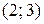 .
.
 2015-04-01
2015-04-01 431
431








