Формулы, сводящие значения тригонометрической функции аргумента 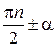 ,
, 
 , к функции аргумента
, к функции аргумента 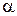 , называют, обычно, формулами приведения.
, называют, обычно, формулами приведения.
Справедливы следующие правила:
1. при переходе от функций углов 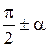 ,
, 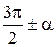 к функциям угла
к функциям угла 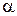 название функции меняют на «ко-функцию»; при переходе от функций углов
название функции меняют на «ко-функцию»; при переходе от функций углов 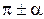 ,
, 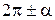 к функциям угла
к функциям угла 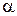 имя функции не меняется;
имя функции не меняется;
2. знак определяется по функции, которую нужно преобразовать.
| Функция | Аргумент | ||||||
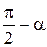 | 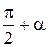 | 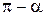 | 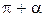 | 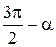 | 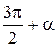 | 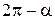 | |
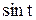 | 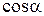 | 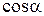 | 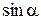 |  | 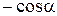 | 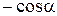 |  |
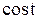 | 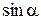 |  | 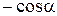 | 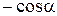 |  | 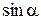 | 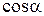 |
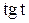 |  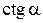 | 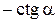 | 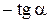 | 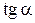 | 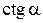 | 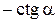 | 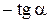 |
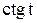 | 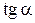 | 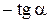 | 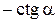 | 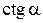 | 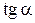 | 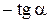 | 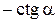 |
Пример 8.1. Найти значение выражения 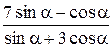 , если
, если 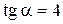 .
.
Решение. 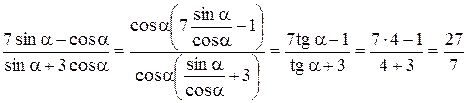 .
.
Ответ: 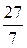 .
.
Пример 8.2. Найти значение выражения 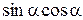 , если
, если 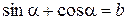 .
.
Решение. Возведем обе части равенства 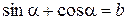 в квадрат, тогда получим:
в квадрат, тогда получим:
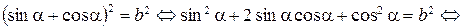
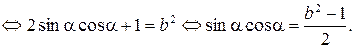
Ответ: 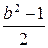 .
.
Пример 8.3. Вычислить: 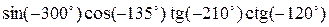 .
.
Решение. Воспользуемся свойствами четности и нечетности тригонометрических функций и формулами приведения для каждого множителя исходного выражения:
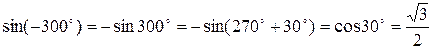 ;
;
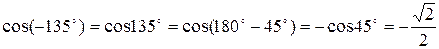 ;
;
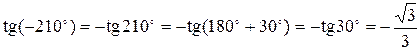 ;
;
 .
.
Следовательно,
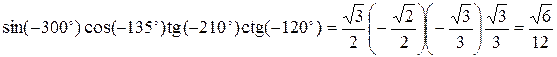 .
.
Ответ: 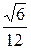 .
.
Пример 8.4. Упростить выражение 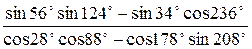 .
.
Решение. Используя формулы приведения, получим
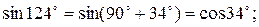 | 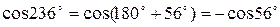 |
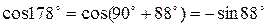 | 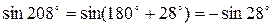 |
Тогда
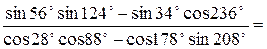
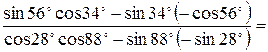
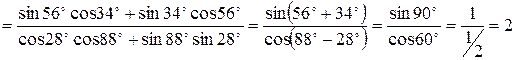 .
.
Ответ: 2.
Пример 8.5. Найти значение выражения 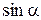 ,
, 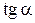 ,
, 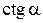 , если
, если 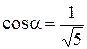 и
и 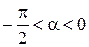 .
.
Решение. Так как 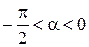 , то
, то 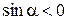 и
и
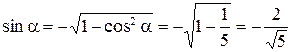 .
.
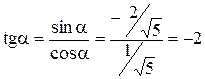 ;
; 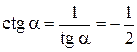 .
.
Ответ: 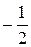 .
.
Пример 8.5. Найти значение выражения 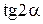 , если
, если 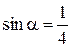 и
и 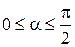 .
.
Решение. Преобразуем первоначально 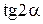 , используя формулы двойного аргумента.
, используя формулы двойного аргумента.
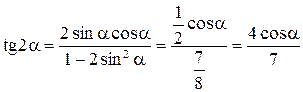 .
.
Вычислим 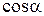 . Так как по условию
. Так как по условию 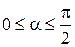 , то
, то 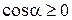 и
и
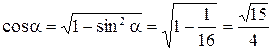 .
.
Ответ: 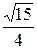 .
.
Пример 8.6. Найти значение выражения 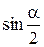 , если
, если 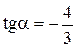 и
и 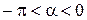 .
.
Решение. Воспользуемся соотношением 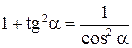 , тогда
, тогда
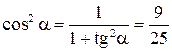 ,
,
откуда 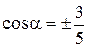 . Так как
. Так как 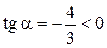 и по условию
и по условию 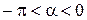 , то
, то 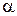 принадлежит четвертой четверти, то есть
принадлежит четвертой четверти, то есть 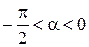 . Тогда
. Тогда 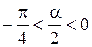 , поэтому
, поэтому 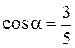 и
и 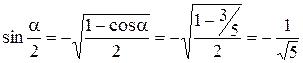 .
.
Ответ: 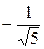 .
.
Пример 8.7. Найти значение выражения 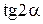 , если
, если 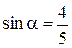 , а
, а 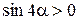 .
.
 2015-04-01
2015-04-01 712
712








