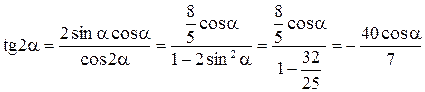 .
.
Найдем 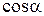 . По условию,
. По условию,
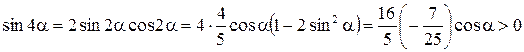 ,
,
следовательно, 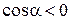 . Тогда получаем
. Тогда получаем
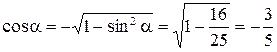 и
и 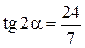 .
.
Ответ: 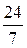 .
.
Пример 8.8. Найти значение выражения 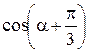 , если
, если 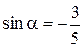 , а
, а 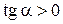 .
.
Решение. Так как по условию 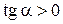 , а
, а 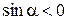 , то
, то 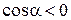 , поэтому
, поэтому 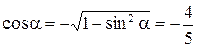 . Тогда имеем
. Тогда имеем
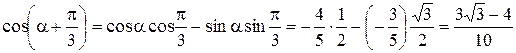 .
.
Ответ: 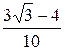 .
.
Пример 8.9. Упростить выражение 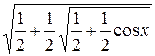 , если
, если 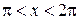 .
.
Решение.
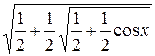
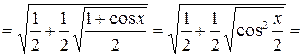
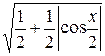 .
.
По условию 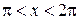 ;
; 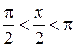 , следовательно,
, следовательно, 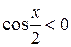 и значит,
и значит,
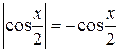 .
.
Тогда
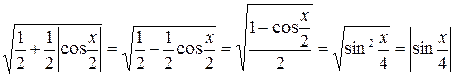 .
.
Из 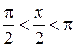 следует, что
следует, что 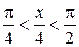 , значит
, значит 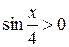 . Тогда
. Тогда
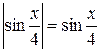 .
.
Ответ: 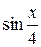 .
.
Определение обратных тригонометрических функций
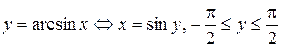 ; ;
| 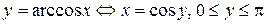 ; ;
|
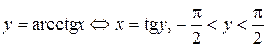 ; ;
| 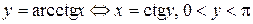 . .
|
Свойства обратных тригонометрических функций
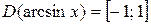
| 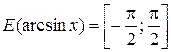
|
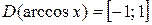
| 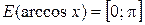
|
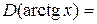 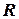
| 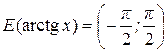
|
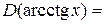 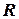
| 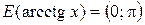
|
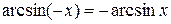
| 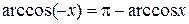
|
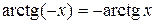
| 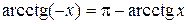
|
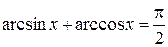 , если , если 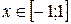
| 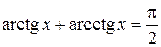
|
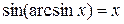 , если , если 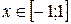 ; ;
| 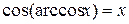 , если , если 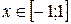
|
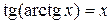
| 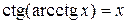
|
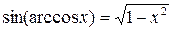
| 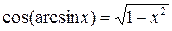
|
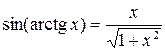
| 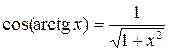
|
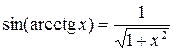
| 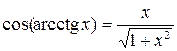
|
Некоторые значения обратных тригонометрических функций
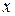
| 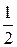
| 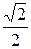
| 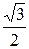
| -1 | ||
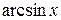
| 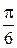
| 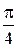
| 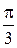
| 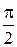
| 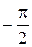
| |
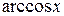
| 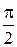
| 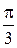
| 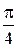
| 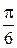
| 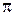
|
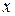
| 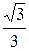
| 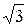
| ||
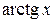
| 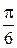
| 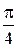
| 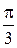
| |
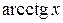
| 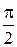
| 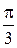
| 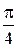
| 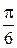
|
 2015-04-01
2015-04-01 230
230








