Определение 8.3. Уравнения, содержащие тригонометрические функции, называются тригонометрическими.
Рассмотрим первоначально основные виды и способы решения простейших тригонометрических уравнений.
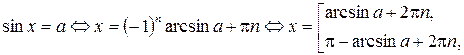 ,
, 
 ,
, 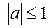 .
.
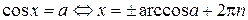 ,
, 
 ,
, 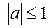 .
.
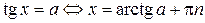 ,
, 
 ,
, 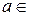
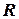 .
.
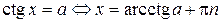 ,
, 
 ,
, 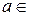
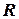 .
.
Пример 8.10. Решить уравнение 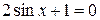 .
.
Решение.
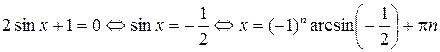 ,
, 


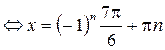 ,
, 
 .
.
Ответ: 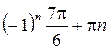 ,
, 
 .
.
Пример 8.11. Решить уравнение 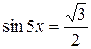 .
.
Решение. 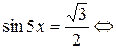
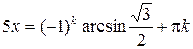 ,
, 


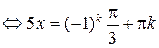 ,
, 


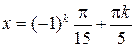 ,
, 
 .
.
Ответ: 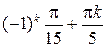 ,
, 
 .
.
Пример 8.12. Решить уравнение 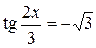 .
.
Решение. 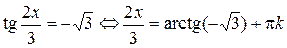 ,
, 


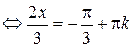 ,
, 


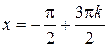 ,
, 
 .
.
Ответ: 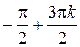 ,
, 
 .
.
Пример 8.13. Решить уравнение 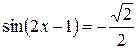 .
.
Решение. 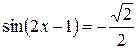
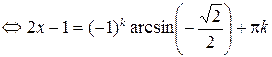 ,
, 


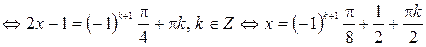 ,
, 
 .
.
Ответ: 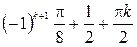 ,
, 
 .
.
Пример 8.14. Решить уравнение 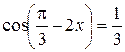 .
.
Решение. Воспользуемся четностью функции 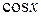 , тогда
, тогда
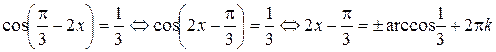 ,
, 


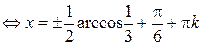 ,
, 
 .
.
Ответ: 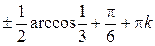 ,
, 
 .
.
Пример 8.15. Решить уравнение 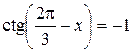 .
.
Решение. Учитывая нечетность функции 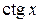 , имеем
, имеем
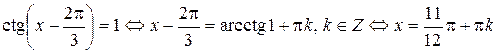 ,
, 
 .
.
Ответ: 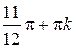 ,
, 
 .
.
Если уравнение не является простейшим, то с помощью тождественных преобразований его нужно привести к одному или нескольким простейшим. Отметим, что не существует единого алгоритма решения тригонометрических уравнений. Выделим некоторые методы решения тригонометрических уравнений.
1. Разложение на множители.
2. Однородные уравнения.
Определение 8.4. Однородными тригонометрическими уравнениями 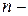 й степени относительно
й степени относительно 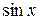 и
и 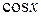 называются уравнения вида:
называются уравнения вида:
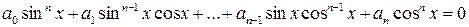 , ,
| (8.3) |
где 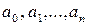 - действительные числа,
- действительные числа, 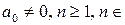
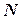 . Сумма показателей степени при
. Сумма показателей степени при 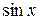 и
и 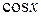 у всех слагаемых уравнений равна
у всех слагаемых уравнений равна 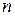 .
.
Замечание 8.1. Отметим, что 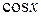 не может быть равен нулю, так как при
не может быть равен нулю, так как при 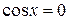 исходное уравнение примет вид:
исходное уравнение примет вид: 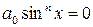 , откуда
, откуда 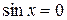 , что невозможно, поскольку
, что невозможно, поскольку 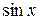 и
и 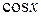 не могут равняться нулю одновременно.
не могут равняться нулю одновременно.
Разделим уравнение (8.3) на 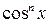 , тогда имеем
, тогда имеем
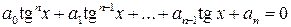 , ,
| (8.4) |
В (8.4) сделаем замену 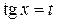 , тогда получим алгебраическое уравнение
, тогда получим алгебраическое уравнение
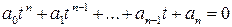 .
.
3. Введение вспомогательного аргумента (при этом используются формулы (8.1), (8.2)).
4. Метод оценки левой и правой части. Такие уравнения решаются путем сведения к системе тригонометрических уравнений.
5. Использование формул понижения степени (формул половинного аргумента).
Пример 8.16. Решить уравнение 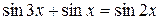 .
.
Решение. 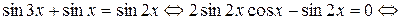
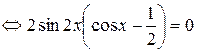
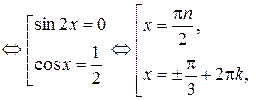
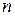 ,
, 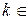
 .
.
Ответ:  ;
; 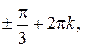
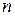 ,
, 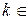
 .
.
Пример 8.17. Решить уравнение 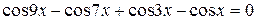 .
.
Решение. 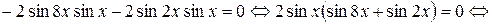
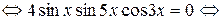
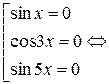
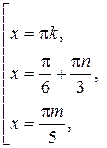
 ,
, 
 .
.
Так как при  ,
, 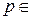
 , решения первого и третьего уравнения совокупности совпадают, то получаем:
, решения первого и третьего уравнения совокупности совпадают, то получаем: 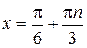 ,
, 
 и
и 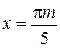 ,
, 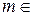
 .
.
Ответ: 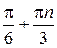 ;
; 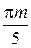 ,
, 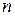 ,
, 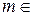
 .
.
Пример 8.18. Решить уравнение
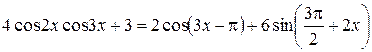 .
.
Решение. Используя четность функции 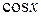 и формулы приведения, получаем
и формулы приведения, получаем
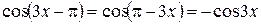 ,
, 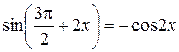 .
.
Тогда исходное уравнения примет вид:
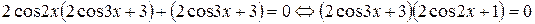 .
.
Так как 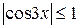 , то
, то 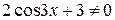 . Тогда из последнего уравнения имеем:
. Тогда из последнего уравнения имеем:
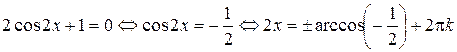 ,
, 


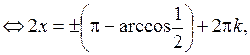



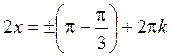 ,
, 



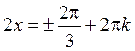 ,
, 


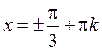 ,
, 
 .
.
Ответ: 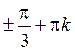 ,
, 
 .
.
Пример 8.19. Решить уравнение 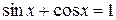 .
.
 2015-04-01
2015-04-01 334
334








