Плоская гармоническая звуковая волна

Решением волнового уравнения:

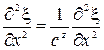
является функция вида:

.

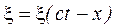Если волна гармоническая, то

,

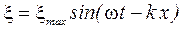где 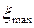- амплитуда смещения частиц в волне;

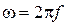- циклическая частота колебаний в волне;

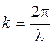- волновое число;

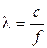- длина звуковой волны.

Скорость колебаний частиц в волне:

,

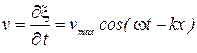где 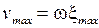- амплитуда колебательной скорости.

Звуковое давление:

,

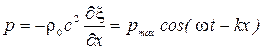где 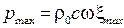- амплитуда звукового давления.

Отметим, что отношение звукового давления к колебательной скорости равно волновому сопротивлению среды .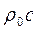

Акустическая добавка к плотности равна:

,

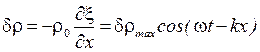где 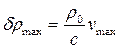- амплитуда акустической добавки к плотности.

Акустическая добавка к температуре:

.

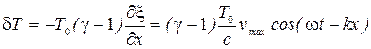Следует отметить, что обычно задаются не амплитудные значения величин, характеризующих звуковые колебательные процессы в среде, а действующие или эффективные, которые при гармонических колебаниях в 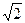раз меньше амплитудных. Например:

.

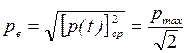Далее индекс e будем опускать и подразумевать, что если задается какая-то конкретная величина (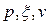 и так далее), то имеется в виду ее эффективное значение.