2015-04-01
369
Покажем, что при расшифровании восстанавливается исходный текст. Согласно обобщению Эйлером малой теоремы Ферма: если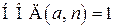 
, то 
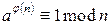, или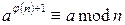 
. Открытый 
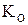и закрытый 
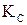ключи в алгоритме связаны соотношением 
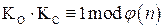, или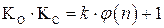 
для некоторого целого 
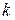. Таким образом, процесс шифрования, а затем расшифрования некоторого сообщения 
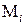выглядит следующим образом:
.
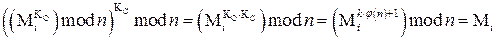В процессе применения RSA злоумышленник может иметь: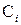 
, , 
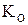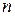– и организовать дешифрование двумя способами:
1. По 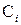, , 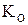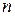получить 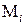. Для этого он решает задачу вычисления 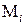из уравнения 
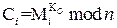. Эта задача вычислительно трудна.
2. По 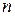вычислить 
, 
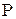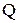, затем найти 
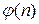и вычислить 
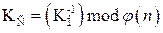и дешифровать сообщение 
.
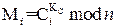Однако задача разложения большого числа на простые множители вычислительно сложна.
Пользователи А и В должны быстро осуществлять все вычисления: вычислять 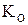, шифровать и расшифровывать.
Вычисление 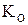с использованием алгоритма Евклида ‑ довольно быстрый процесс и не представляет трудности. Шифровывание и расшифрование ‑ возведение большого числа в большую степень ‑ требует определенных затрат времени, но, с учетом наличия быстрых алгоритмов и быстродействия современных компьютеров, это приемлемая процедура.
