В модели Солоу экономика рассматривается как единое целое (без структурных подразделений), в ней производится единственный продукт, который может потребляться как в непроизводственной сфере, так и производственной. Потребление его в производственной сфере может рассматриваться как инвестирование. Эта модель достаточно адекватно отражает важнейшие макроэкономические аспекты, в том числе и процесса воспроизводства.
Состояние экономики в модели Солоу задается пятью переменными состояния: Y - конечный продукт, L - трудовые ресурсы, K - производственные фонды, I - инвестиция, C - непроизводственное потребление. Все переменные взаимосвязано изменяются во времени, т.е. являются функциями времени.
Считается, что производственные и трудовые ресурсы используются полностью. В качестве K и L берутся их среднегодовые значения. В качестве момента времени t принимается середина года. Тогда конечный продукт в каждый момент времени является функцией среднегодовых фондов и труда Y = f(K, L) (1). Таким образом, Y = f(K, L) - производственная функция всего народного хозяйства.
Конечный продукт используется на непроизводственное потребление и инвестиции: Y = C + I. Норма накопления (доля инвестиции в конечном продукте) обозначим через r, тогда I = rY, C = (1 – r)Y (2). В дальнейшем норма накопления считается постоянной. Она меняется в пределах 0 < r < 1. Инвестиции используются на восстановление выбывших фондов и на их прирост, поэтому dK/dt = rY – mK, K(0) = K 0(3). Если считать, что прирост трудовых ресурсов пропорционален наличным трудовым ресурсам, то будем иметь dL/dt = nL. Решение этого дифференциального уравнения дает решение L = L 0 ent (4), L 0 - трудовые ресурсы в начале наблюдения, при t = 0.
Таким образом, модель Солоу задается системой уравнений (1)-(4) Вводя среднюю фондовооруженность k = K/L и f(k) = F(k, 1 ), для k получим дифференциальное уравнение dk/dt = rf(k) – (m + n)k, k(0) = K 0 /L 0 (5).
Уравнение (5) - это уравнение с разделяющимися переменными и начальным условием, поэтому оно имеет единственное решение.
увеличение цены приводит к уменьшению количества покупаемых товаров и наоборот.
Рассмотрим стационарную траекторию, т.е. такую, на которой фондовооруженность постоянна и является решением уравнения rf(k) – (m + n)k = 0. При этом из уравнений (1)-(4) получается, что на стационарной траектории все основные макропоказатели растут экспоненциально ent, пропорционально трудовым ресурсам.
Для производственной функции Кобба-Дугласа уравнение (5) точно решается, которое при больших значениях t стремится к стационарному решению.
Расчеты показывают, что оптимальная норма r в стационарном режиме равна коэффициенту эластичности по фондам a («золотое правило» экономического роста). Но это справедливо для производственной функции Кобба-Дугласа.
Тесты по теме №8
1.Транспортная задача (см. рисунок) будет закрытой, если…
£ a=50, b=60
£ a=50, b=65
£ a=50, b=75
Ra=50, b=70
2.Область допустимых решений задачи линейного программирования имеет вид (см.рисунок). Тогда максимальное значение функции 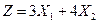 равно…
равно…
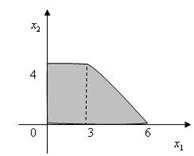
£ 24
£ 16
R25
£ 27
3.Область допустимых решений задачи линейного программирования имеет вид (см. рисунок). Тогда максимальное значение функции (см.рисунок) равно…
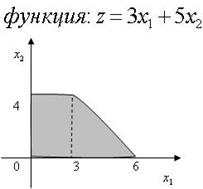
R29
£ 27
£ 20
£ 31
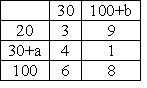
4.Транспортная задача(см. таблицу). Будет закрытой, если…
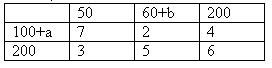
R a=45, b=35
£a=45, b=25
£ a=45, b=40
£ a=45, b=30
5. Матрица выигрышей в игре с природой имеет вид (см. рисунок). Тогда наибольший средний выигрыш достигается при применении…
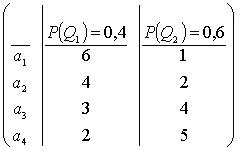
£ стратегии a2
£ стратегии a4
£ стратегии a1
R стратегии a3
6.Матрица выигрышей в игре с природой имеет вид: (см. рисунок). Тогда наибольший средний выигрыш достигается при применении…
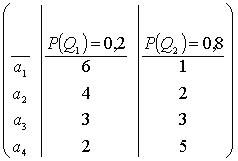
£ стратегии a[1]
R стратегии a[3]
£ стратегии a[2]
£ стратегии a[4]
7.Даны функции спроса и предложения, где р-цена товара. Тогда равновесный объем "спроса-предложения" равен...
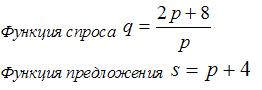
£ 8
£10
£ 6
R 2
8.Даны функции спроса и предложения, где р - цена товара. Тогда равновесный объем "спроса-предложения" равен...
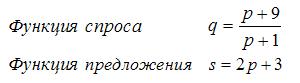
£ 9
R 1
£ 5
£ 15
 2015-04-01
2015-04-01 2229
2229








