Трехмерные преобразования и проекции

Рассмотрим трехмерную декартовую систему координат, являющуюся правосторонней. Примем соглашение, в соответствии с которым, будем счи­тать положительными такие повороты, при которых (если смотреть с конца полуоси в направлении начала координат) поворот на 90° против часовой стрелки будет переводить одну полу­ось в дру­гую. На основе этого соглаше­ния строится следующая таблица, которую можно исполь­зовать как для пра­вых, так и для левых систем координат:

Если ось вращения	Положительным будет направление поворота
X	От y к z
Y	От z к x
Z	От x к y

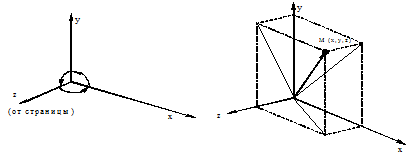
Рис. 3.6 Трехмерная система координат

Аналогично тому, как точка на плоскости описывается вектором (x,y), точка в трехмерном пространстве описы­вается вектором (x,y,z).

Как и в двухмерном случае, для возможности реализаций трехмерных пре­образований с помощью матриц пе­рейдем к однородным координатам:

[x,y,x,1] или [X,Y,Z,H]

[x*,y*,z*1] = [ 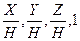], где Н¹1, ¹0

Обобщенная матрица преобразования 4´4 для трехмерных однородных ко­ординат имеет вид

Т=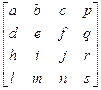

Эта матрица может быть представлена в виде 4-х отдельных частей:

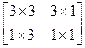
· Матрица 3´3 осуществляет линейное[1] преобразование в виде изменения масштаба, сдвига и вращения.

· Матрица 1´3 производит перенос

· Матрица 3´1- преобразования в перспективе

· Скалярный элемент 1´1 выполняет общее изменение масштаба

Рассмотрим воздействие матрица 4´4 на однородный вектор [ x,y,z,1 ]

1) Трехмерный перенос – является простым расширением двумерного:

T(Dx,Dy,Dz) =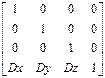

т.е. [x,y,z,1]*T(Dx,Dy,Dz)=[x+Dx,y+Dy,z+Dz,1]

2) Трехмерное изменение масштаба

Рассмотрим частичное изменение масштаба. Оно реализуется следующим образом:

S(Sx,Sy,Sz,)=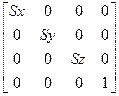

т.е. [x,y,z,1]*S(Sx,Sy,Sz)=[Sx*x,Sy*y,Sz*z,1]

Общее изменение масштаба получается за счет 4-ого диагонального эле­мента, т.е.:

[x y z 1] * = [x y z S] = [x* y* z* 1] = [ ]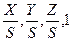

Такой же результат можно получить при равных коэффициентах частичных изменений масштабов. В этом случае матрица преобразования такова:

S=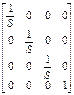

3) Трехмерный сдвиг

Недиагональные элементы матрицы 3´3 осуществляют сдвиг в 3-х измере­ниях, т.е.

[x y z 1]* 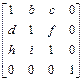=[x+yd+hz, bx+y+iz, cx+fy+z, 1]

4) Трехмерное вращение

Двухмерный поворот, рассмотренный ранее, является в то же время трех­мерным пово­ротом вокруг оси Z. В 3-х мерном пространстве поворот во­круг оси Z описывается мат­рицей

Rz()=

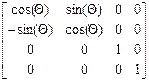
Матрица поворота вокруг оси X имеет вид

Rx()=

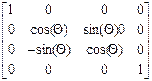
Матрица поворота вокруг оси Y имеет вид

Ry()=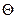

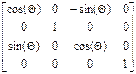
Результатом произвольной последовательности поворотов вокруг осей x, y, z является матрица

А=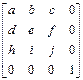

Подматрицу 3´3 называют ортогональной, т.к. ее столбцы являются вза­имно ортогональными един. векторами.

Матрицы поворота сохраняют длину и углы, а матрицы масштабирования и сдвига нет.