По данному конечному автомату А можно найти наименьший эквивалентный ему автомат (автомат с минимальным числом состояний). Для этого исключаются недостижимые состояния и склеиваются лишние состояния. Лишние состояния определяются с помощью разбиения множества всех достижимых состояний на классы эквивалентности так, что любой класс содержит неразличимые состояния. После этого их любого класса берется по одному представителю. Таким образом, можно сократить автомат, если он содержит недостижимые состояния или 2 или более неразличимых состояний.
Пусть А - конечный автомат, z1, z2 - два его состояния. Цепь a различает z1 и z2, если из состояния z1 можно перейти в z3 под действием конечного числа тактов:
(z1, a) |––––* (z3, e)
и из состояния z2 можно перейти в z4 под действием конечного числа тактов:
(z2, a) |––––* (z4, e)
причем или z3, или z4 принадлежит множеству заключительных состояний:
z3/z4 Î F.
Состояния z1 и z2 будем называть k-неразличимыми, если не существует такой цепочки a, различающей z1 и z2, длина которой меньше или равна k:
z1 ºk z2
Состояния z1 и z2 будем называть неразличимыми, если они k-неразличимы для всех k>= 0.
z1 º z2
Автомат А называется приведенным, если в его множестве состояний нет недостижимых состояний и нет 2-х неразличимых состояний.
Пример:
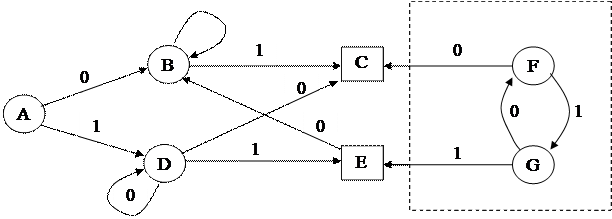 |
Недостижимые состояния - F и G (из А никогда не попадешь в F и G).
Теорема: Пусть А - конечный автомат с n-состояниями. Состояния z1 и z2 неразличимы тогда и только тогда, когда они (n-2)-неразличимы:
z1 ºn-2 z2
Вопросы и упражнения
Пусть A= (Z, X, t, z0, F),
Z - множество состояний = {z0, z1, z2, zF}
X= {0, 1}
F= {zF}
t:
| z0 | z1 | zF |
| z1 | z1 zF | z1 |
| z2 | z2 | z2 zF |
| zF | – | – |
Постройте граф данного автомата.
Является ли данный автомат детерминированным?
Можно ли минимизировать данный автомат?
 2015-04-01
2015-04-01 1192
1192
