Даундэйтинг термов

Удалить терм – значит исключить терм из базы данных, или, в случае ЛСИ, удаление ряда из матрицы, ассоциированного с удаляемым термом из существующего вектора термов в U_k. Как было сказано, k-наибольшие сингулярные значения å_k и соответствующие сингулярные вектора (столбцы в матрицах U_k и V_k) используются для создания матрицы уменьшенного ранга A_k , которая может быть записана как

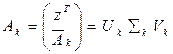, (16)

где z^T - первый ряд из A_k , требующий удаления. Определим ε₁ как вектор-столбец размерностью m x 1, состоящий из всех нулей, кроме первого элемента, чье значение равно 1, и определим ортогональную матрицу Û размерностью m x (k + 1) заданную как

Û = [U_k | s ],

где s – вектор размерности mx1, ортогональный к U_k.

То есть U^Т_k s = 0.

Тогда

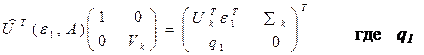(17)

Первый столбец матрицы, расположенной справа в выражении 21, обозначим за Н. Он, в сущности, представляет собой первый ряд матрицы U_k, и следующий за ним первый элемент s. Матрицы вращения G_l и G_r Гивенса (левая и правая) могут быть построены так:

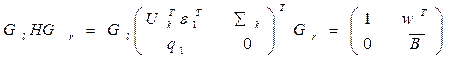, (18)

где `В – верхняя бидиагональная матрица размерностью k x k. Используя последние два ненулевых значения в первом столбце матрицы Н, вращение Гивенса может быть определено так, что левое умножение на ортогональную матрицу эффективно обнуляет последние ненулевые вхождения в первом столбце. Вращение Гивенса устанавливает только один поворот, который определяет серии вращений, аккумулированных в ортогональной G_l матрице размерностью (k + 1) х (k + 1).

Левое умножение на вращение Гивенса, конечно, может ввести ненулевой элемент над наддиагональю модифицированной матрицы Н. Такие вхождения могут быть обнулены соответственным вращением Гивенса, примененным к правой стороне матрицы Н (или к ее столбцам).

Правое умножение матрицы Н на данное вращение Гивенса (аккумулированное в ортогональной G_l матрице размерностью (k + 1) х (k + 1)), в свою очередь, может вызвать появление ненулевых элементов ниже диагонали матрицы Н, и для удаления этого требуется левое умножение на другое вращение Гивенса.

Такая последовательность левых и правых умножений на вращение Гивенса продолжается пока все ненулевые элементы, появляющиеся ниже диагонали или выше наддиагонали в Н, вытесняются из правого нижнего угла матрицы Н для создания результирующей двух-диагональной матрицы `В [8]. Используя выражение (22), можно показать, что сингулярные значения матрицы `В размером k x k такие же, что и у матрицы A_k из формулы (20). Если же ортогональные матрицы G_l и G_r размером (k + 1) x (k + 1) определены как

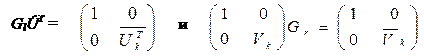то из этого следует:

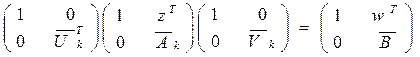. (19)

Следовательно, второй ряд в выражении (23) наследует обновленную удалением бидиагональную форму матрицы `А_k , то есть

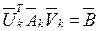. (20)

Бидиагональная матрица `В размером k x k может быть диагонализирована [10]. Эта процедура выдаст на выходе диагональную матрицу, составленную из сингулярных значений, эквивалентных сингулярным значениям из `В и из обновленной удалением матрицы A_k из выражения (24). Здесь же,

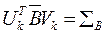(21)

где U_B и V_B ортогональные матрицы размером k x k, созданные с помощью преобразования Гивенса. Из выражений (24) и (25) следует:

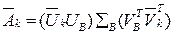, (22)

что терм, данный как z в выражении (20), был обновлен удалением и новая модель ЛСИ можно записать как:

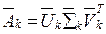(23)

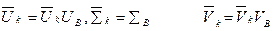где

Любой ряд матрицы A_k из выражения (20) может быть обновлен удалением используя вышеописанный процесс. Выбранный ряд может быть передвинут на место первого для унификации с представлением матрицы A_k из выражения (20). Для даундэйтинга более чем одного ряда, процесс применяется итеративно. Результирующие матрицы `А<sub>k</sub>, `U_k, `V<sub>k</sub>, и `∑_k отражают изменения в семантической модели, используемой ЛСИ.