7.1. Гармонический сигнал
Гармонический сигнал 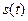 записывают в виде
записывают в виде
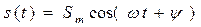 , (7.1)
, (7.1)
где 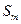 - амплитуда сигнала (индекс
- амплитуда сигнала (индекс 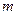 от слова «максимум»),
от слова «максимум»), 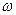 - круговая частота, а
- круговая частота, а 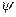 - начальная фаза. Временная диаграмма гармонического сигнала
- начальная фаза. Временная диаграмма гармонического сигнала 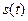 показана на рис. 7.1.
показана на рис. 7.1.

Рис. 7.1
Амплитуда гармонического сигнала – это его максимальное значение, она измеряется в единицах сигнала (вольтах для напряжения и амперах для тока).
Период сигнала 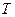 (рис. 7.1) определяет циклическую частоту
(рис. 7.1) определяет циклическую частоту 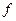 его повторения,
его повторения,
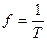 , (7.2)
, (7.2)
измеряемую в герцах (Гц). Ее физический смысл – число периодов колебаний в секунду.
Аргумент косинуса в (7.1) вида
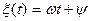 (7.3)
(7.3)
называют полной фазой колебания, она пропорциональна текущему времени и измеряется в радианах или градусах.
Круговая частота 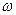 равна
равна
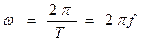 (7.4)
(7.4)
и представляет собой число радиан, на которое изменяется полная фаза колебания в единицу времени (1 с).
При 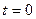 полная фаза равна
полная фаза равна 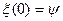 , поэтому параметр
, поэтому параметр 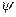 называют начальной фазой гармонического сигнала. Она измеряется в радианах или градусах. Так как период функции
называют начальной фазой гармонического сигнала. Она измеряется в радианах или градусах. Так как период функции 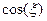 равен
равен 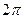 или 3600, то начальная фаза оказывается многозначной величиной. Например, значения начальной фазы 300 и (300+3600)=3900, а также (300-3600)=-3300 оказываются эквивалентными. Для устранения неоднозначности договариваются, что значения начальной фазы должны находиться, например, в интервале от 0 до
или 3600, то начальная фаза оказывается многозначной величиной. Например, значения начальной фазы 300 и (300+3600)=3900, а также (300-3600)=-3300 оказываются эквивалентными. Для устранения неоднозначности договариваются, что значения начальной фазы должны находиться, например, в интервале от 0 до 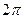 , или от
, или от 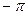 до
до 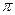 (аналогичные границы могут быть заданы в градусах).
(аналогичные границы могут быть заданы в градусах).
Начальная фаза связана со смещением гармонического сигнала во времени на величину 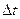 относительно функции
относительно функции 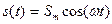 , как показано на рис. 7.1. Функция
, как показано на рис. 7.1. Функция 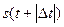 смещена влево относительно
смещена влево относительно 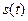 , а
, а 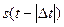 - вправо. Положительные значения
- вправо. Положительные значения 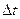 отсчитываются в сторону увеличения
отсчитываются в сторону увеличения 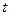 , а отрицательные – наоборот. Из (7.1) можно записать
, а отрицательные – наоборот. Из (7.1) можно записать
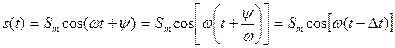 , (7.5)
, (7.5)
где смещение во времени 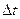 равно
равно
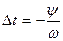 . (7.6)
. (7.6)
Тогда для начальной фазы получим
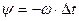 . (7.7)
. (7.7)
Как видно, начальная фаза определяется временным сдвигом 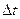 гармонического сигнала относительно функции
гармонического сигнала относительно функции 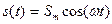 . При
. При 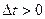 сигнал
сигнал 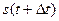 смещается вправо (позднее сигнала
смещается вправо (позднее сигнала 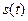 ) по оси времени, при этом его начальная фаза
) по оси времени, при этом его начальная фаза 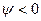 , а если
, а если 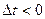 , то временная диаграмма смещается влево (раньше
, то временная диаграмма смещается влево (раньше 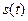 ) по оси времени, а
) по оси времени, а 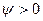 .
.
Величина начальной фазы зависит от начала отсчета времени (положения точки 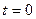 ). При смещении начала отсчета времени изменяется и начальная фаза.
). При смещении начала отсчета времени изменяется и начальная фаза.
Применительно к двум гармоническим сигналам 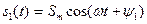 и
и  с разными начальными фазами
с разными начальными фазами 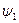 и
и 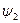 вводится в рассмотрение сдвиг фаз между первым и вторым сигналами,
вводится в рассмотрение сдвиг фаз между первым и вторым сигналами,
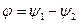 . (7.8)
. (7.8)
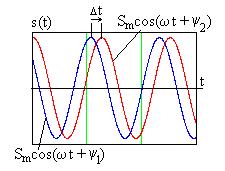
На рис. 7.2 показаны два гармонических сигнала с начальными фазами 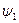 и
и 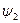 , причем
, причем 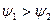 и
и 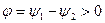 . В этом случае говорят, что первый сигнал опережает по фазе второй или второй сигнал отстает по фазе от первого.
. В этом случае говорят, что первый сигнал опережает по фазе второй или второй сигнал отстает по фазе от первого.
Сдвиг фаз 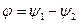 связан со смещением
связан со смещением 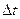 сигналов во времени
сигналов во времени
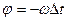 , (7.9)
, (7.9)
 положительные значения временного сдвига отсчитываются в направлении оси времени. Гармоническое колебание может быть задано в нетипичной форме, которую необходимо преобразовать к виду (7.1), иначе начальная фаза
положительные значения временного сдвига отсчитываются в направлении оси времени. Гармоническое колебание может быть задано в нетипичной форме, которую необходимо преобразовать к виду (7.1), иначе начальная фаза
Рис. 7.2 оказывается неопреде-
ленной. Примеры преобразования показаны в табл. 7.1.
Таблица 7.1.
| Исходный сигнал | Преобразованный сигнал | Начальная фаза |
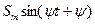 | 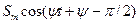 | 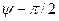 |
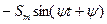 | 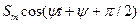 | 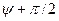 |
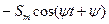 | 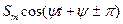 | 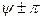 |
7.2. Схемотехническое моделирование
Рассмотрим цепь, показанную на рис. 7.3 при e(t) = E sin(wt), E = 1 В, Re = 1 кОм, f = 50 кГц, 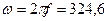 рад/с.
рад/с.
. 
Рис. 7.3
Построим модель цепи в программе MicroCAP, показанную на рис. 7.4.

Рис. 7.4
На рис. 7.5 показаны временные диаграммы напряжений источника e(t) (кривая с самой большой амплитудой), напряжения 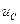 в узле 2 (на емкости
в узле 2 (на емкости 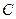 и сопротивлении
и сопротивлении  ) и напряжения
) и напряжения 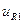 на сопротивлении
на сопротивлении 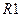 .
.

Рис. 7.5
По кривым на рис. 7.5 определяются амплитуды напряжений и их сдвиги во времени относительно напряжения источника, значения которых приведены в табл. 7.2.
Начальные фазы связаны со сдвигом во времени соотношением
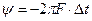 ,
,
результаты расчетов приведены в табл. 7.2.
Таблица 7.2
| Элемент | U, В | 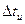 мкс мкс | 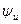 рад рад |
| V1 | |||
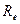 | 0,29 | 0,785 | |
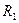 , , 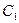 | 0,85 | -2,5 | -0,314 |
Уравнение второго закона Кирхгофа имеет вид
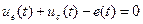 .
.
Обозначим левую часть уравнения
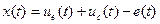 .
.
При точных расчетах выполняется условие 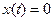 , а при приближенных (округленных) результатах моделирования появляется погрешность
, а при приближенных (округленных) результатах моделирования появляется погрешность 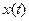 , которую можно представить графически. Программа расчета в программе MathCAD показана на рис. 7.6, а результаты - на рис. 7.7.
, которую можно представить графически. Программа расчета в программе MathCAD показана на рис. 7.6, а результаты - на рис. 7.7.
Аналогичные результаты необходимо получить для токов в элементах цепи и проверить выполнение первого закона Кирхгофа. Требуется исследовать фазовые соотношения между токами и напряжениями в элементах цепи.
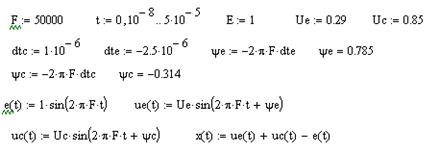
Рис. 7.6
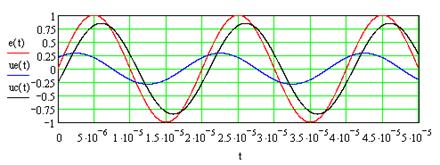
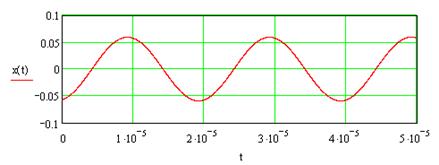
Рис. 7.7
Как видно, временные диаграммы напряжений в верхней части рис.7.7 совпадают с результатами моделирования. Из графика 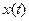 в нижней части рис. 7.7 следует, что погрешность выполнения второго закона Кирхгофа меняется по гар-
в нижней части рис. 7.7 следует, что погрешность выполнения второго закона Кирхгофа меняется по гар-
моническому закону с амплитудой 0,06 В (6 % от амплитуды напряжения источника), что обусловлено погрешностями измерения амплитуд и начальных фаз напряжений по результатам моделирования.
ПРИЛОЖЕНИЕ
Таблица двоичных кодов номера студента
| N | N2 | N | N2 | N | N2 | N | N2 |
 2015-04-01
2015-04-01 4800
4800








