Определение. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции F= 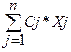 (1)
(1)
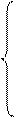 при условиях
при условиях 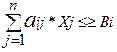 i=
i= 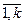
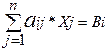 i=
i= 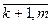 (2)
(2)
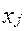 ≥ 0 j=
≥ 0 j= 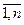
Вектор 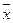 (x1,x2…xn), удовлетворяющий системе ограничений (2), называется допустимым решением задачи линейного программирования (ЗЛП) или планом задачи. Вектор
(x1,x2…xn), удовлетворяющий системе ограничений (2), называется допустимым решением задачи линейного программирования (ЗЛП) или планом задачи. Вектор 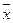 , являющийся допустимым решением ЗЛП, при котором целевая функция (1) достигает оптимального значения, называется оптимальным решением ЗЛП.
, являющийся допустимым решением ЗЛП, при котором целевая функция (1) достигает оптимального значения, называется оптимальным решением ЗЛП.
Пример. Простейшая задача планирования производства. Предприятие располагает m видами ресурсов и может выпускать продукцию n различными технологическими способами. За единицу времени использования j технологического способа расходуется Aij единиц i-го ресурса, при этом выпускается γj единиц продукции. Требуется запланировать работу предприятия так, чтобы выпустить максимальное количество продукции, если ресурса i-го вида в наличии не более Bi единиц.
Составим математическую модель задачи. Пусть Хj – время использования j-й технологии, тогда 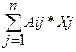 – количество ресурса i-го вида, необходимого для всего производства, тогда система ограничений и целевая функция примут вид:
– количество ресурса i-го вида, необходимого для всего производства, тогда система ограничений и целевая функция примут вид:
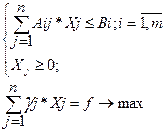
Используем возможность геометрической интерпретации для случая двух переменных х1 и х2. Целевая функция вида F(x1, x2)=γ1x1+γ2x2→ opt может быть изображена графически в виде семейства прямых, которые имеют один и тот же вектор нормали 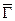 (γ1,γ2). Перемещая одну из прямых в направлении вектора
(γ1,γ2). Перемещая одну из прямых в направлении вектора 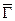 (для задачи максимизации) или в направлении, противоположном вектору
(для задачи максимизации) или в направлении, противоположном вектору 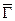 (для задачи минимизации), получим наивысшую (наинизшую) точку пересечения области Ω допустимых решений с прямой уровня – решение задачи максимизации (минимизации).
(для задачи минимизации), получим наивысшую (наинизшую) точку пересечения области Ω допустимых решений с прямой уровня – решение задачи максимизации (минимизации).
Пример. Известно, что затраты сырья вида I, II, III при способах производства 1 и 2, а также запасы сырья каждого вида составляют:
| Способ производства | Затраты сырья при использовании соответствующих способов производства (кг/ч) | Выпуск продукции за 1ч. | ||
| I | II | III | ||
| Запасы сырья (кг) |
Найти план производства, при котором будет выпушено наибольшее кол-во продукции.
Решение. Пусть x1, х2 – время использования 1-го и 2-го способа производства, тогда система ограничений примет вид:
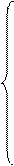 10x1+20x2≤100 – затраты 1-го вида сырья при использовании 1-го и 2-го способа производства
10x1+20x2≤100 – затраты 1-го вида сырья при использовании 1-го и 2-го способа производства
20x1+10x2≤100 – затраты 2-го вида сырья при использовании 1-го и 2-го способа производства
15x1+15x2≤90 – затраты 3-го вида сырья использовании 1-го и 2-го способа производства
x1,x2 ≥0 – требования наличия физического смысла переменных.
Целевая функция, отражающая количество выпущенной продукции, имеет вид: F(x1,x2)=20x1+30x2 → max
Изобразим систему ограничений задачи и вектор нормали Г, соответствующий целевой функции на координатной плоскости:
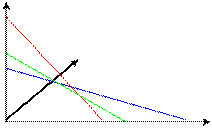 x2
x2
6 Г (2,3)
5 6 10 x1
оптимальное решение α опт получено как точка пересечения прямых 10x1+20x2=100 и15x1+15x2=90, поэтому решим систему уравнений:
 10x1+20x2=100, x1=2,
10x1+20x2=100, x1=2,
15x1+15x2=90; x2=4.
Итак, αопт (2,4); т.е. для максимизации количества произведенной продукции 2 часа нужно использовать первый способ производства и 4 часа – второй способ, тогда обеспечим max F(x1,x2)= F(2,4)=20*2+30*4=160 – кол-во единиц выпущенной продукции.
2 Решение задач линейного программирования симплекс-методом
Определение. ЗЛП вида
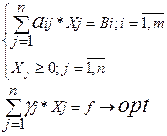
называется основной задачей линейного программирования.
Определение. Если каждое уравнение системы ограничений основной ЗЛП приведено к такому виду, что одна переменная входит с коэффициентом 1 только в одно уравнение и с коэффициентом 0 - во все другие уравнения (эти переменные называются базисными, а остальные переменные называются свободными), причем это условие выполняется для каждого уравнения, а целевая функция выражена только через свободные переменные, тогда ЗЛП называется приведенной к базису или записанной в каноническом виде:
F= C0+C1*x1+…+Cn*xk → opt
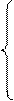 a11*X1+a12*X2+…+a1k*Xk +Xk+1=b1
a11*X1+a12*X2+…+a1k*Xk +Xk+1=b1
a21*X1+a22*X2+…+a2k*Xk +Xk+2 =b2 (*)
…
ak1*X1+ak2*X2+…+akk*Xk +X2k =bk
Хi≥0
Xk+1, Xk+2, …, X2k – базисные переменные;
X1, X2, … Xk – свободные переменные.
Определение. Векторы 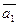 =
= 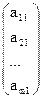 ,
, 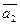 =
= 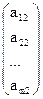 , …,
, …, 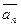 =
= 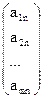 называются
называются
векторами-условиями,
вектор 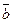 =
= 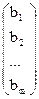 называется вектором-ограничением основной задачи линейного программирования.
называется вектором-ограничением основной задачи линейного программирования.
Определение. Опорным решением задачи линейного программирования называется допустимое решение 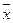 задачи линейного программирования в основной форме, если векторы условий
задачи линейного программирования в основной форме, если векторы условий 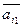 ,
, 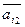 , …,
, …, 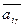 образуют линейно независимую систему, где i1, i2, …, ir – номера всех ненулевых координат вектора
образуют линейно независимую систему, где i1, i2, …, ir – номера всех ненулевых координат вектора 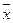 опорного решения.
опорного решения.
Определение. Для задачи линейного программирования в каноническом виде (*) таблица
| Базис | Х0 | Х1 | Х2 | … | Хk | Хk+1 | Хk+2 | … | Хn |
| Хк+1 | b1 | a11 | a12 | … | a1k | … | |||
| Xк+2 | b2 | a21 | a22 | … | a2k | … | |||
| … | … | … | … | … | … | … | … | … | … |
| Xn | bk | ak1 | ak2 | … | akk | … | |||
| оценки | C0 | -C1 | -C2 | … | -Ck | … |
называется симплекс-таблицей.
Заметим, что строка оценок является строкой, содержащей оценки базиса хk+1, хk+2, … х2k для опорного решения, причем значение функции
F(αопорное)= С0
 2015-04-01
2015-04-01 1017
1017
