1. Весом набора 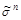 называется число единиц в данном наборе. Сколько существует наборов
называется число единиц в данном наборе. Сколько существует наборов 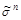 веса k?
веса k?
2. Найти номера наборов (1001), (01101), (110010).
3. Найти вектор длины 6, являющийся двоичным разложением числа 19.
4. Восстановить таблицу истинности функции 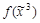 =41.
=41.
5. Частичная функция не определена на k наборах. Сколько существует различных доопределений данной функции?
6. Выяснить, какие из ниже перечисленных выражений являются формулами над множеством связок {ù,&,Ú,®}:
1) x ® y; 4) (x ® y)®ù x; 7) (ù x ® z);
2) (x &)ù z; 5) (x & yy)ù y; 8) (x ®(y &(ù x)));
3) (x ® y)ù x; 6) y &(z ®(x Úù y)).
7. Проверить справедливость формул (4.1) и (4.2).
8. Построить таблицу функций, реализуемых следующими формулами:
1) 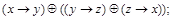 3)
3) 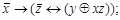
2) 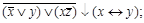 4)
4) 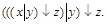
9. Эквивалентны ли формулы 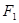 и
и 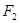 ?
?
1) 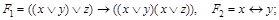
2) 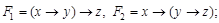
3) 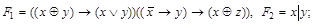
4) 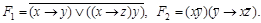
10. Написать программу, определяющую вес двоичного набора, который хранится в машинном слове b. Содержимое b интерпретируется машиной как беззнаковое целое.
Указание. Необходимо организовать подсчет единичных разрядов в машинном слове. Это можно сделать, выполнив n раз сдвиг влево (вправо) и анализ (n -1)-го (0-го) бита слова, где n - длина слова. Число шагов такого алгоритма всегда равно n и не зависит от веса двоичного набора. Более оригинальный алгоритм подсчета числа единичных разрядов в слове всегда делает k шагов, где k – число единиц в слове. Он основан на том, что операция b:= b and (b -1) уничтожает в b самую правую единицу, т.о., после того, как указанная операция будет выполнена k раз, слово станет нулевым (b =0).
4.1.2 Булева алгебра. Эквивалентные преобразования формул.
Двойственные и самодвойственные функции. Алгебра жегалкина
Алгебра 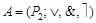 , основным множеством которой является все множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй.
, основным множеством которой является все множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй.
Операции алгебры А называют булевыми операциями. Формулы над множеством {Ú,&,ù} также называют булевыми формулами. Тот факт, что любая логическая функция может быть представлена в виде формулы над {Ú,&,ù}, будет доказан ниже.
Рассмотрим основные свойства булевых операций.
Ассоциативность:
а) 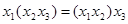 ; б)
; б) 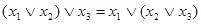 . (4.3)
. (4.3)
Коммутативность:
а)  ; б)
; б) 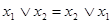 . (4.4)
. (4.4)
Дистрибутивность конъюнкции относительно дизъюнкции:
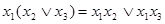 . (4.5)
. (4.5)
Дистрибутивность дизъюнкции относительно конъюнкции:
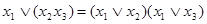 . (4.6)
. (4.6)
Идемпотентность:
а) 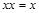 ; б)
; б) 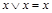 . (4.7)
. (4.7)
Двойное отрицание:
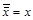 . (4.8)
. (4.8)
Свойства констант:
а) x &1= x; б) x &0=0; в) x Ú1=1;
г) x Ú0= x; д)  =1; е)
=1; е) 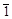 =0. (4.9)
=0. (4.9)
Правила де Моргана:
а) 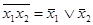 ; б)
; б) 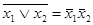 . (4.10)
. (4.10)
Закон противоречия:
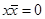 . (4.11)
. (4.11)
Закон "исключения третьего":
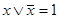 . (4.12)
. (4.12)
Соотношения (4.3) – (4.12) можно проверить указанным ранее стандартным методом – вычислением обеих частей равенств на всех наборах значений переменных. Очевидно, что результат вычисления не зависит от того, как получены значения переменных, входящих в эти равенства, то есть, от того, являются ли эти переменные независимыми, или, в свою очередь, получены в результате каких-то вычислений.
Поэтому равенства (4.3) - (4.12) остаются справедливыми при подстановке вместо переменных любых логических функций и, следовательно, любых формул, представляющих эти функции. Важно лишь соблюдать следующее правило подстановки формулы вместо переменной: при подстановке формулы F вместо переменной x все вхождения переменной x в исходное соотношение должны быть одновременно заменены формулой F.
Сформулируем также правило замены подформул, которое позволяет, используя эквивалентные соотношения, получать формулы, эквивалентные данной. Пусть 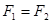 , тогда, если какая-либо формула F содержит
, тогда, если какая-либо формула F содержит 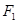 в качестве подформулы, то замена
в качестве подформулы, то замена 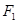 на
на 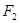 не изменяет F.
не изменяет F.
Подчеркнем разницу между правилами подстановки и замены. При подстановке переменная заменяется на формулу; формула может быть любой, но требуется одновременная ее подстановка вместо всех вхождений переменной. При замене подформул может быть заменена любая подформула, однако, не на любую другую, а только на эквивалентную ей. При этом, замена всех вхождений исходной подформулы не обязательна.
Такие преобразования, использующие эквивалентные соотношения и правило замены, называются эквивалентными преобразованиями.
Запас эквивалентных соотношений можно расширить с помощью правила подстановки.
Пример 4.1. Возьмем соотношение 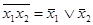 (4.10а) и подставим
(4.10а) и подставим 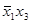 вместо
вместо 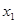 . Получим
. Получим 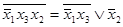 , то есть две формулы, не эквивалентные исходным, но эквивалентные между собой. Если же в правой части нового соотношения
, то есть две формулы, не эквивалентные исходным, но эквивалентные между собой. Если же в правой части нового соотношения 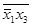 заменить формулой
заменить формулой 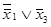 , эквивалентной ей в силу (4.10а), а в полученной подформуле
, эквивалентной ей в силу (4.10а), а в полученной подформуле 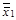 заменить на эквивалентную ей в силу (4.8) формулу
заменить на эквивалентную ей в силу (4.8) формулу 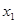 , то все формулы в построенной цепи преобразований
, то все формулы в построенной цепи преобразований 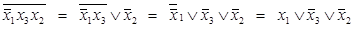 эквивалентны.
эквивалентны.
Рассмотрим некоторые из эквивалентных соотношений в булевой алгебре, и как они получаются путем использования уже рассмотренных соотношений.
Правила поглощения:
а) 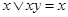 ; б)
; б) 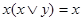 . (4.13)
. (4.13)
Для доказательства первого равенства используются последовательно соотношения (4.9а), (4.5), (4.9в), (4.9а): 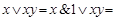
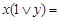
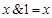 . Второе равенство доказывается с помощью (4.5), (4.7а) и первого равенства:
. Второе равенство доказывается с помощью (4.5), (4.7а) и первого равенства: 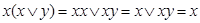 .
.
Правило склеивания:
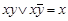 . (4.14)
. (4.14)
Доказательство: 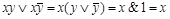 .
.
Правило обобщенного склеивания:
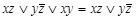 . (4.15)
. (4.15)
Доказывается с помощью расщепления, то есть, применения (4.14) в обратную сторону и поглощения (4.13а): 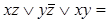
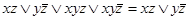 .
.
Правило вычеркивания:
а) 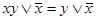 ; б)
; б) 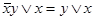 ; (4.16)
; (4.16)
Доказательство: 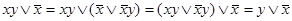 ;
;
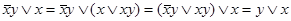 .
.
Эквивалентные преобразования являются мощным средством доказательства эквивалентности формул, как правило, более эффективным, чем их вычисление на наборах значений переменных.
Пример 4.2. Эквивалентны ли формулы 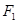 и
и 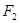 ?
?
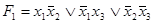 ;
; 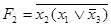 .
.
Используя последовательно (4.18), (4.15), (4.14) и (4.13а), получаем
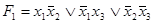 =
= 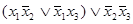 =
= 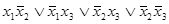 =
= 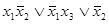 =
= 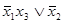 .
.
Теперь преобразуем 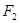 с помощью соотношений (4.10а), (4.10б) и (4.4б):
с помощью соотношений (4.10а), (4.10б) и (4.4б):
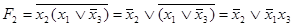 =
= 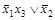 .
.
Т.о., формулы 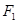 и
и 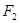 эквивалентны.
эквивалентны.
Для более легкого запоминания рассмотренных соотношений, и получения новых можно использовать принцип двойственности.
Функция 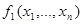 называется двойственной к функции
называется двойственной к функции 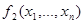 , если
, если 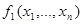 =
= 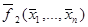 .
.
Может оказаться, что функция двойственна самой себе, т.е., 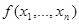 =
= 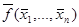 . В этом случае она называется самодвойственной функцией.
. В этом случае она называется самодвойственной функцией.
Принцип двойственности заключается в следующем: если в формуле F, представляющей функцию f, все знаки функций заменить соответственно на знаки двойственных функций, то полученная формула F* будет представлять функцию f*, двойственную f.
Для формул над множеством {0,1,ù,&,Ú} принцип двойственности может быть сформулирован так: для получения формулы F *, двойственной формуле F, достаточно в формуле F всюду заменить 0 на 1, 1 на 0, & на Ú, Ú на &.
Например, из соотношения 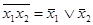 применением принципа двойственности получается соотношение
применением принципа двойственности получается соотношение 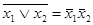 .
.
Пример 4.3. Является ли функция 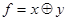 двойственной к функции
двойственной к функции 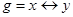 ?
?
Проверку двойственности и самодвойственности функций можно производить непосредственно по их таблицам истинности или с помощью эквивалентных преобразований. Проведем проверку по таблицам истинности (табл. 4.6, 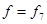 ,
, 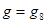 ). Имеем
). Имеем 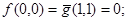
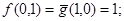
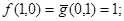
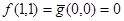 . Т.о. функция f двойственна к функции g.
. Т.о. функция f двойственна к функции g.
Пример 4.4. Является ли функция 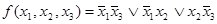 самодвойственной?
самодвойственной?
Для ответа на поставленный вопрос с помощью эквивалентных преобразований докажем, что 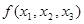 =
= 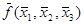 .
.
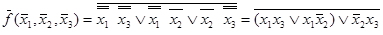 =
= 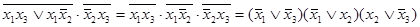
Заметим, что тот же результат можно было получить, используя принцип двойственности, сформулированный для формул над множеством {0,1,ù,&,Ú}. Продолжим эквивалентные преобразования:
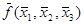 =
= 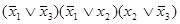 =
= 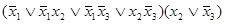 =
= 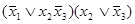 =
= 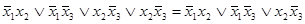 .
.
Т.о., 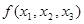 =
= 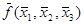 , следовательно, функция f самодвойственная. Рассмотрим еще одну алгебру над множеством логических функций. Алгебра над множеством логических функций с двумя бинарными операциями & и Å называется алгеброй Жегалкина. В алгебре Жегалкина выполняются следующие соотношения:
, следовательно, функция f самодвойственная. Рассмотрим еще одну алгебру над множеством логических функций. Алгебра над множеством логических функций с двумя бинарными операциями & и Å называется алгеброй Жегалкина. В алгебре Жегалкина выполняются следующие соотношения:
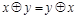 ; (4.17)
; (4.17)
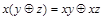 ; (4.18)
; (4.18)
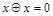 ; (4.19)
; (4.19)
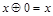 , (4.20)
, (4.20)
а также соотношения булевой алгебры, относящиеся к конъюнкции и константам (4.3а), (4.4а), (4.7а), (4.9а), (4.9б).
Отрицание и дизъюнкция выражаются так:
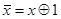 ; (4.21)
; (4.21)
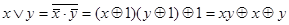 . (4.22)
. (4.22)
Любая булева функция может быть представлена формулой над множеством 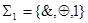 . Это следует из того, что любая булева функция может быть представлена формулой над множеством
. Это следует из того, что любая булева функция может быть представлена формулой над множеством 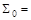 {ù,&,Ú} (см. разд. 4.2) и того, что функции {ù, &, Ú} выражаются через функции {&,Å,1} (см. (4.21), (4.22)).
{ù,&,Ú} (см. разд. 4.2) и того, что функции {ù, &, Ú} выражаются через функции {&,Å,1} (см. (4.21), (4.22)).
Пример 4.5. Эквивалентны ли формулы 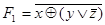 и
и 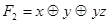 ?
?
Преобразуем 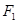 . Используя соотношение (4.22), получаем
. Используя соотношение (4.22), получаем
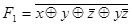 .
.
Далее, с помощью соотношения (4.21) избавимся от отрицаний и раскроем скобки (4.18):
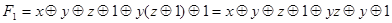 .
.
Используя соотношения (4.19) и (4.20), окончательно получаем:
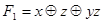 .
.
Т.о., формула 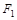 эквивалентна формуле
эквивалентна формуле 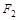 .
.
 2015-04-01
2015-04-01 1757
1757








