Воспользовавшись теоремой 4.1 при 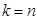 , получаем представление
, получаем представление
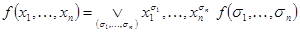 ,
,
которое для 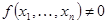 может быть преобразовано к виду
может быть преобразовано к виду
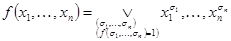 , (4.25)
, (4.25)
где дизъюнкция берется по всем наборам 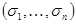 , на которых
, на которых 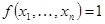 .
.
Разложение функции 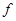 по всем переменным (4.25) называют предельным разложением или совершенной дизъюнктивной нормальной формой (СДНФ) функции
по всем переменным (4.25) называют предельным разложением или совершенной дизъюнктивной нормальной формой (СДНФ) функции 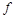 . СДНФ функции
. СДНФ функции 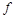 содержит ровно столько конъюнкций, сколько единиц в таблице функции
содержит ровно столько конъюнкций, сколько единиц в таблице функции 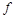 , каждому единичному набору
, каждому единичному набору 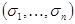 соответствует конъюнкция всех переменных, в которых
соответствует конъюнкция всех переменных, в которых 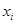 взято с отрицанием, если
взято с отрицанием, если 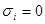 , и без отрицания, если
, и без отрицания, если 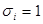 . Например, набору
. Например, набору  соответствует конъюнкция
соответствует конъюнкция 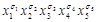 =
= 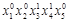 =
= 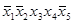 . Такую конъюнкцию еще называют конституентой единицы. Другими словами, СДНФ – это дизъюнкция конституент единицы, соответствующих единичным наборам функции.
. Такую конъюнкцию еще называют конституентой единицы. Другими словами, СДНФ – это дизъюнкция конституент единицы, соответствующих единичным наборам функции.
Таким образом, существует взаимно однозначное соответствие между таблицей функции 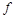 и ее СДНФ, и, следовательно, СДНФ для всякой логической функции единственна (точнее, единственна с точностью до порядка букв и конъюнкций: это означает, что ввиду коммутативности дизъюнкции и конъюнкции, формулы, полученные из (4.25) перестановкой конъюнкций и букв в конъюнкции, не различаются и считаются одной и той же СДНФ). Например, функции, заданные табл. 4.7, имеют СДНФ:
и ее СДНФ, и, следовательно, СДНФ для всякой логической функции единственна (точнее, единственна с точностью до порядка букв и конъюнкций: это означает, что ввиду коммутативности дизъюнкции и конъюнкции, формулы, полученные из (4.25) перестановкой конъюнкций и букв в конъюнкции, не различаются и считаются одной и той же СДНФ). Например, функции, заданные табл. 4.7, имеют СДНФ:
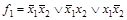 ,
,
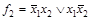 ,
,
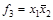 .
.
Единственная функция, не имеющая СДНФ – это константа 0.
Таблица 4.7
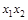 | 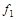 | 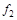 | 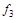 |
| 0 0 | |||
| 0 1 | |||
| 1 0 | |||
| 1 1 |
Теорема 4.2. Всякая логическая функция может быть представлена булевой формулой, то есть, как суперпозиция дизъюнкции, конъюнкции и отрицания.
Доказательство: Как было сказано выше, всякую логическую функцию, кроме константы 0, можно представить СДНФ, которая является булевой формулой. Константу 0 можно представить в виде булевой формулы 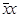 . Таким образом, любую логическую функцию можно представить булевой формулой. Теорема доказана.
. Таким образом, любую логическую функцию можно представить булевой формулой. Теорема доказана.
Так как СДНФ для логической функции единственна, то иногда, для установления эквивалентности формул удобно формулы привести с СДНФ и произвести их сравнение.
Пример 4.6. Эквивалентны ли формулы 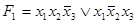 и
и 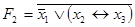 ?
?
Формула 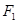 является СДНФ, так как представляет собой дизъюнкцию двух конституент единицы. По определению эквивалентности (
является СДНФ, так как представляет собой дизъюнкцию двух конституент единицы. По определению эквивалентности (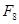 в табл. 4.6) получим ее представление в СДНФ:
в табл. 4.6) получим ее представление в СДНФ: 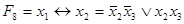 . Используя представление эквивалентности в СДНФ и соотношения булевой алгебры, преобразуем в СДНФ
. Используя представление эквивалентности в СДНФ и соотношения булевой алгебры, преобразуем в СДНФ 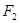 :
:
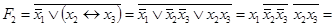
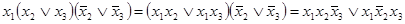 ,
,
т. е. формулы 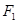 и
и 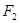 эквивалентны.
эквивалентны.
Используя принцип двойственности, выпишем двойственное предельное разложение:
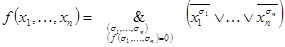 ,
,
которое называется совершенной конъюнктивной нормальной формой (СКНФ) функции 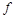 . СКНФ функции
. СКНФ функции 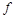 содержит ровно столько дизъюнкций, сколько нулей в таблице функции
содержит ровно столько дизъюнкций, сколько нулей в таблице функции 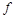 , каждому нулевому набору
, каждому нулевому набору 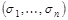 соответствует дизъюнкция всех переменных, в которых
соответствует дизъюнкция всех переменных, в которых 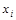 взято без отрицания, если
взято без отрицания, если 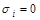 , и с отрицанием, если
, и с отрицанием, если 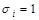 . Например, набору
. Например, набору 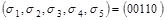 соответствует дизъюнкция
соответствует дизъюнкция 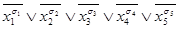 =
= 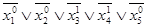 =
= 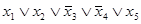 . Для такой дизъюнкции еще употребляется название конституента нуля. То есть СКНФ представляется как конъюнкция конституент нуля, соответствующих нулевым наборам функции. Следовательно, между таблицей и СКНФ также существует взаимно однозначное соответствие. Например, функции, заданные табл.4.7, имеют СКНФ:
. Для такой дизъюнкции еще употребляется название конституента нуля. То есть СКНФ представляется как конъюнкция конституент нуля, соответствующих нулевым наборам функции. Следовательно, между таблицей и СКНФ также существует взаимно однозначное соответствие. Например, функции, заданные табл.4.7, имеют СКНФ:
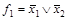 ,
,
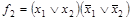 ,
,
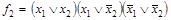 .
.
 2015-04-01
2015-04-01 1542
1542








