Общее правило составления уравнений Колмогорова

Список литературы 70

Введение

Основным современным методом исследования телекоммуникационных систем (ТС) на всех стадиях их разработки, проектирования и модернизации является моделирование.

Модель является представлением объекта, системы или понятия в некоторой форме, отличной от формы их реального существования.

Модель — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.

Модель может определяться как структура для хранения знаний об объекте.

Модель объекта может быть или точной копией этого объекта или отображать некоторые характерные свойства объекта в абстрактной форме. Модель служит обычно средством, помогающим нам в объяснении, понимании или совершенствовании системы. В настоящее время моделирование становится не только эффективным методом научных исследований сложных объектов, но и мощным инструментом конструирования и проектирования сложных систем. Качество решений задач, получаемых с помощью математического моделирования, определяется степенью адекватности модели реальному объекту, (т.е. насколько результаты моделирования соответствуют результатам работы реального объекта). Результат моделирования зависит от степени адекватности модели, правильности исходных предпосылок, умения исследователя правильно применять используемые методы, правильной интерпретации результатов.

Методами моделирования решаются важнейшие задачи анализа и синтеза телекоммуникационных систем (ТС). Моделирование дает возможность разработчику системы экспериментировать с системой (существующей или предполагаемой) в тех случаях, когда делать это на реальном объекте нецелесообразно или невозможно. По результатам моделирования могут быть построены исчерпывающие зависимости между параметрами ТС и функционалами, характеризующими её свойства; исследованы закономерности и решены задачи, сведенные с выбором оптимальных параметров и построения рациональной стратегии управления.

Математическая модель ТС представляет собой математическое описание основных процессов функционирования системы. По своей структуре математическая модель системы состоит из модели взаимодействия элементов между собой, а также моделей внешних воздействий на систему.

Важнейшим свойством является его универсальность. Этот метод в принципе не требует создания специальной аппаратуры для каждой новой задачи, он позволяет относительно просто изменять числовые значения параметров, начальных условий и режимов работы исследуемых (создаваемых) ТС. Методологически математическое моделирование разбивается на два вида: аналитическое и имитационное моделирование.

При аналитическом моделировании математическая модель реализуется в виде такой системы уравнений относительно искомых величин, которая допускает получение нужного результата аналитически (в явном виде) или численным методом. В некоторых случаях аналитическое описание системы становится чрезмерно сложным, что затрудняет получение требуемых результатов. В данной ситуации следует переходить к использованию имитационных моделей.

Имитационная модель в принципе позволяет воспроизвести весь процесс функционирования ТС с сохранением логической структуры, связи между явлениями и последовательность протекания их во времени.

При имитационном моделировании на компьютере имитируется работа проектируемой системы. Математическая модель при этом реализуется в виде программы для компьютера. В результате экспериментов на компьютере собирается статистика, обрабатывается и выдается необходимая информация. Таким образом, можно получить характеристики проектируемой системы, исследовать факторы, влияющие на них.

Для имитационного моделирования разработаны специальные системы моделирования. Системы моделирования имеют специализированные средства, позволяющие организовать модельные эксперименты на компьютере, учитывающие в моделях фактор времени. В них имеются языки моделирования, ориентированные на определенную предметную область.

Одной из систем моделирования, применяемых в отрасли телекоммуникаций, является GPSS World.

Первая и вторая глава учебного пособия посвящены вопросам аналитического моделирования ТС методами теории систем массового обслуживания.

В третьей главе рассмотрены основы имитационного моделирования ТС на языке GPSS World.

Четвертая глава посвящена вопросам планирования экспериментов, организации проведения компьютерного моделирования.

1 Основы теории систем массового обслуживания

1.1 Общие сведения о системах массового обслуживания (СМО)

Одним из важных разделов математического моделирования является теория систем массового обслуживания.

Основоположником теории является датский математик А. К. Эрланг. Являясь сотрудником Копенгагенской телефонной компании, он опубликовал в 1909г работу «Теория вероятностей и телефонные переговоры», в которой впервые поставил и решил некоторые задачи теории систем массового обслуживания.

Каждая система массового обслуживания (СМО) включает в свою структуру некоторое число обслуживающих устройств, которые называют каналами обслуживания. Роль каналов могут играть различные приборы, линии связи, лица, выполняющие те или иные операции (кассиры, операторы, продавцы),

Системы массового обслуживания могут быть одноканальными или многоканальными.

Каждая СМО предназначена для обслуживания некоторого потока заявок, поступающих на вход системы в случайные моменты времени. Обслуживание заявок длится случайное время. После обслуживания заявки канал освобождается и готов к приему следующей заявки.

Случайный характер потока заявок и времени их обслуживания приводит к неравномерной загруженности СМО: в некоторые промежутки времени на входе скапливаются заявки, становятся в очередь на обслуживание, либо покидают систему.

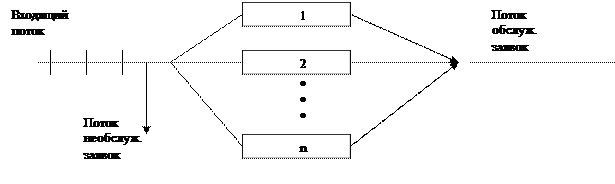
Рисунок 1.1 – Схема СМО

Таким образом, во всякой СМО можно выделить следующие основные элементы:

а) входящий поток заявок;

б) очередь;

в) каналы обслуживания;

г) выходящий поток обслуженных заявок;

д) поток необслуженных заявок.

Примерами СМО могут служить телефонные станции, билетные кассы, магазины, парикмахерские и т. д.

Каждая СМО в зависимости от своих параметров: характеристик потока заявок, числа каналов обслуживания и их производительности, а также от правил организации работы обладает определенной эффективностью функционирования (качеством обслуживания).

Предметом теории массового обслуживания является установление зависимости между характером потока заявок, числом каналов, их производительностью, правилами работы СМО и эффективностью функционирования.

Задачи теории массового обслуживания – нахождение вероятностей различных состояний СМО, а также установление зависимости между заданными параметрами (числом каналов n, интенсивностью потока заявок l, и т. д.) и характеристиками качества работы СМО. Характеристиками качества работы СМО могут быть:

- среднее число заявок, обслуживаемое в единицу времени, или пропускная способность СМО;

- вероятность обслуживания поступившей заявки;

- вероятность отказа в обслуживании;

- среднее число заявок в СМО;

- среднее число заявок в очереди;

- среднее время пребывания заявки в СМО;

- среднее время пребывания заявки в очереди;

- среднее число занятых каналов.

Исследование любой СМО начинается с рассмотрения потоков заявок, поступающих на вход СМО, на вход канала обслуживания и покидающих СМО.

1.2 Модели потоков событий

Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени.

Примерами могут быть:

- поток вызовов на телефонной станции;

- поток грузовых составов, поступающих на железнодорожную станцию;

- поток сбоев компьютера;

- поток выстрелов, направляемых на цель, и т.д.

Потоки событий обладают многообразными свойствами, которые позволяют выделять различные типы потоков.

Регулярным потоком называется поток, в котором события следуют одно за другим через одинаковые промежутки времени (детерминированная последовательность событий).

Такой поток событий редко встречается на практике. В телекоммуникационных системах чаще встречаются потоки, для которых и моменты наступления событий и промежутки времени между ними являются случайными.

Рассмотрим такие свойства потоков событий, как стационарность, ординарность и отсутствие последействия.

Поток стационарен, если вероятность появления какого-то числа событий на интервале времени τ зависит только от длины этого интервала и не зависит от его расположения на оси времени. Для стационарного потока среднее число событий в единицу времени постоянно.

Ординарным потоком называется поток, для которого вероятность попадания на данный малый отрезок времени 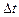двух и более требований пренебрежительно мала по сравнению с вероятностью попадания одного требования. Так, поток клиентов в парикмахерскую — ординарный. Поток клиентов в бюро обмена жилплощади — неординарный, т.к. в зависимости от обмена могут одновременно приходить два, три и более клиента.

Потокбез последствия характеризуется тем, что для двух непересекающихся интервалов времени

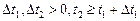
вероятность появления числа событий 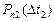на втором интервале не зависит от числа появления событий 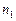на первом интервале. Здесь отсутствует вероятностная зависимость последующего течения процесса от предыдущего. Например, поток покупателей, входящих в магазин, является потоком без последствия, а поток деталей, сходящих с конвейера, является потоком с последействием (детали выходят не чаще, чем через интервал ).

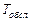Интенсивностью потока называется предел

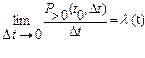
где 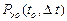— вероятность того, что на интервале 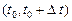появятся заявки.

Для стационарного потока его интенсивность не зависит от времени и равна среднему числу событий в единицу времени: .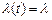

Простейшим или пуассоновским потоком называется поток, обладающий тремя свойствами: ординарностью, отсутствием последействия и стационарностью. Простейший поток занимает центральное место среди всех потоков: существует предельная теорема, согласно которой сумма большого числа независимых потоков с любым законом распределения приближается к простейшему потоку с ростом слагаемых потоков.

Пуассоновским поток называется потому, что подчиняется пуассоновскому закону распределения

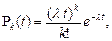
где 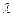— интенсивность потока;

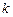— количество событий, появляющихся за время .

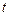Тогда вероятность появления одного события за малое время 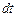равна

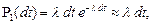
а вероятность того, что за малое время 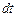не появится ни одно событие, учитывая условие ординарности, равна

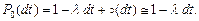
Время между двумя последовательными наступлениями событий потока имеет экспоненциальную функцию распределения

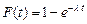или .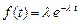

Для показательного распределения

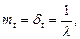
где 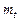— математическое ожидание;

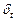— среднеквадратическое отклонение интервалов времени,

т.е. среднее время между наступлениями событий обратно пропорционально интенсивности потока.

1.3 Обзор методов решения задач массового обслуживания

Фундаментальным вероятностным понятием, используемым в теории массового обслуживания, является марковский процесс. Это процесс, дальнейшее поведение которого определяется только его состоянием в данный момент времени и не зависит от предыстории процесса. Состояние системы в общем случае характеризуется некоторым вектором. Чем меньше компонентов содержит вектор состояний, тем легче исследовать поведение процесса.

Наиболее просто обстоит дело при простейшем входном потоке с интенсивностью 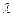и показательном распределении времени обслуживания с интенсивностью 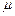. В этом случае элементарные вероятности обслуживания одной из находящихся в системе заявок или прибытия еще одной заявки полностью определяются числом находящихся в системе заявок 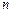(независимо от уже истекших времени обслуживания и интервала с момента поступления), и вектор состояний сводится к скаляру .

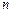Если в одноканальной системе одно из распределений не является показательным, его можно заменить распределением Эрланга с тем же средним 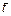и близкой дисперсией 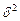. Подбор параметров производится по формулам

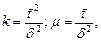
причем 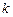должно быть целым, а 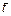— средний интервал между требованиями.

После такой замены обслуживание представляется как последовательное прохождение 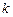фаз, в каждой из которых его продолжительность подчиняется распределению 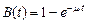. Таким образом, в новой постановке мы имеем дело с марковским процессом, состояние которого характеризуется суммарным числом не пройденных фаз обслуживания, в котором поток заявок является простейшим с требованием объема .

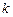Для удобства изложения начальных сведений об исследуемых моделях американским ученым Кендаллом были предложены символические обозначения СМО. Символика использует до шести разрядов. Первый разряд определяет поступающий поток вызовов, второй - закон распределения времени обслуживания, третий - структуру системы обслуживания, четвертый -дисциплину обслуживания, пятый - способ выбора из очереди, шестой - порядок занятия свободных приборов.

В первом разряде используются следующие символы:

M – экспоненциальное распределение промежутка между вызовами;

D – детерминированное распределение;

Eⁿ- эрланговское n – го порядка;

HMⁿ– гиперэранговское n – го порядка;

Gl – произвольное распределение;

Mi - примитивный поток.

Во втором разряде используются те же символы, но они уже обозначают распределения времени обслуживания. Только вместо Gl используется просто G.

Стрелка над симолом соответствует многомерному случаю. Например, M_n означает поступление n простейших потоков.

В третьем разряде используются следующие символы:

S – произвольная структура;

FM – полнодоступная система (Full Matrix), иногда используется v - число приборов;

G – неполнодоступная система (Grading);

HG – равномерная неполнодоступная система;

PG – ступенчатая неполнодоступная система;

Иногда для обозначения неполнодоступной системы используются D - доступность, g – число нагрузочных групп. Многозвенные системы обозначаются символом LS (Link System).

В четвертом разряде используются следующие символы:

LL - дисциплина обслуживания без потерь (Lossles);

L – обслуживание с явными потерями (Loss);

W – обслуживание с ожиданием (Wait);

R – обслуживание с повторением (Reattemt).

В пятом разряде символики указывается способ выбора из очереди в системе с ожиданием:

SP (Same Probability) - равновероятный, FF (First – in – First – out) –упорядоченный (первый пришел – первый ушел), LF (Last – in – First – out) - стековый или магазинный (последний пришел – первый ушел), PR (Priority) – приоритетный.

Шестой разряд символики используется в тех моделях, где требуется указать порядок занятия свободных приборов или путей. При последовательном занятии применяется символ S, при случайном – R.

1.4 Процесс обслуживания как марковский случайный процесс

Пусть система может находиться в состояниях 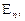где 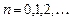— в системе находится 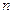заявок. Обозначим вероятность нахождения системы в конкретном состоянии 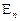в момент времени 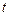через 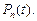Очевидно, что для каждого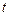

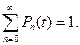
Если переход из состояния 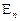в 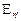зависит только от этих состояний и не зависит от предыдущих 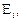то такая последовательность во времени будет марковским процессом. Таким образом, система с ожиданием в случае простейшего потока и показательного времени обслуживания представляет собой случайный процесс Маркова.

Каждой паре состояний 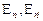можно поставить в соответствие условную вероятность 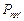того, что система находится в состоянии 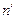в момент 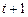при условии, что в момент 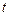она находилась в состоянии .

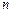Очевидно, что для вероятности 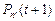можно написать

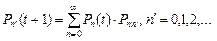(1.1)

Это уравнение означает, что система может оказаться в состоянии 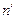путем одного из многих 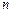несовместных переходов. Причем вероятность нахождения системы в состоянии 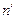при условии, что ранее система находилась в состоянии n, по формуле произведения вероятностей событий, равна 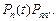Если 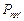равна нулю, то переход из состояния 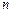в 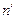невозможен.

Соотношение (1.1) может быть записано в векторной форме

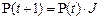, (1.2)

где квадратная матрица 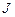образована из элементов 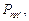удовлетворяющих условиям:

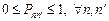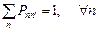Из условия ординарности входного потока следует, что в каждый момент времени может прийти не более одной заявки и покинуть систему не более одной заявки. Отсюда,

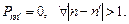
Матрица, удовлетворяющая этим условиям, называется матрицей переходов, вероятности 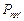— вероятности перехода. Из (1.2) следует, что для однородной последовательности Маркова, определяемой как последовательность, для которой значения элементов матрицы 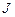постоянны (не зависят от номеров состояний), имеем

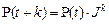в частности,

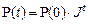т.е. марковская последовательность целиком определяется матрицей перехода 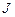и начальными условиями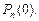

1.5 Одноканальная СМО с ожиданием

Пусть имеется одноканальная система с простейшим потоком на входе с интенсивностью 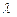и экспоненциальным временем обслуживания с показателем 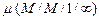. 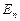— состояние системы, когда в ней находится n заявок. За момент времени 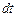может прийти одна заявка с вероятностью 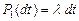; ноль заявок с вероятностью 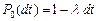, может быть обслужена одна заявка с вероятностью 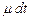и не обслужена ни одна заявка с вероятностью .

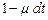Вероятность 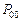определяется вероятностью отсутствия прихода заявок за время 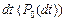. Вероятность 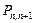определяется вероятностью прихода одной заявки 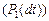, а вероятность 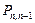определяется вероятностью обслуживания одной заявки. Вероятность 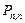определяется вероятностью составного события: заявка не придет и не будет обслужена.

Матрица переходов 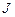будет выглядеть следующим образом

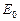
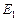
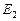
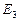
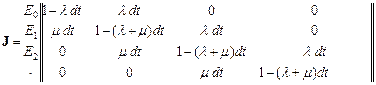
Более компактно матрицу перехода можно представить в виде графа переходов, в котором вершины означают состояния системы, а дуги — вероятности переходов:

...

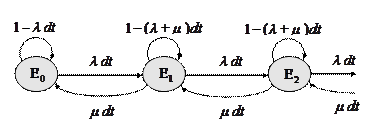Рисунок 1.2 – Граф переходов

Из графа переходов могут быть получены дифференциальные уравнения для вероятностей состояний, которые называются уравнениями Колмогорова.

Общее правило составления уравнений Колмогорова.

В левой части уравнения стоит производная вероятности 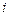-го состояния; в правой части — сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного ( 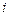-го) состояния.

Построим по этому правилу систему дифференциальных уравнений

...

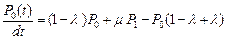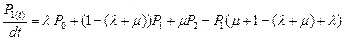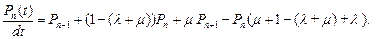
После преобразований получаем

...

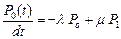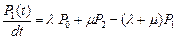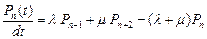Эти уравнения могут быть решены при начальных условиях

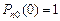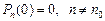
частотными методами с использованием преобразования Лапласа.

Чаще интересуются установившимся или стационарным режимом, для которого справедливо

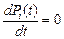В этом случае система дифференциальных уравнений преобразуется в систему линейных уравнений

...

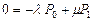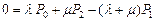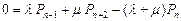отсюда , , .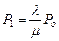

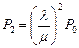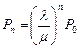Учитывая, что 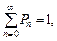получаем

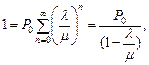
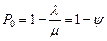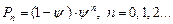
Параметр 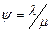выражает степень насыщения в системе и называется загрузкой или коэффициентом использования СМО. Для одноканальных СМО при 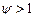установившегося режима не существует, очередь растет неограниченно.