Агрегирование

Пусть производственная система (объединение) состоит из n различных по технологии производств, производственные функции которых имеют вид (см. лекцию 2):

Р_i=a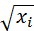_{i ,} i= .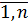

Построим производственную функцию объединения

Р=Ф(Х),

Эта функция должна описывать оптимальную (!) зависимость максимально возможного суммарного объема произведенной продукции от суммарного объема затрачиваемых ресурсов.

Таким образом, построение этой ПФ тесно связано с решением следующей задачи оптимизации распределения ресурсов по технологиям:

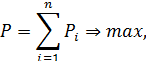
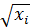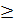P_i=a_i , x_i 0, i= ,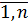

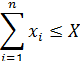
Как было показано выше, решение этой задачи имеет вид:

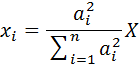
Соответственно

P_i=a_i =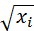

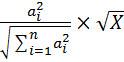
Отсюда следует, что

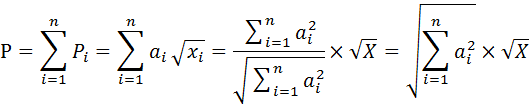
Обозначим

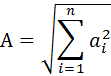
Окончательно получим (агрегированную) ПФ объединения

P=A ,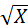

Где А- коэффициент экономической эффективности затрат ресурсов для всего объединения.

Для иллюстрации приведем числовой пример.

Пусть n=2, a₁=3,a₂=4.

Тогда А=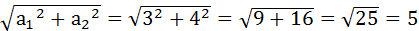

Значит Р=5 .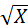

Заметим, что в этом примере, как и в общем случае анализируемой ПФ имеем:

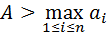
То есть при оптимальном распределении ресурсов «осредненная» по объединению технология эффективнее самой эффективной технологии.

Таким образом, ПФ выражает зависимость произведенной продукции от объема затрачиваемых ресурсов при оптимальном их использовании как в технологическом, так и в экономическом смысле.