Примеры. Пример. Пусть множество U представляет собой стандартный симплекс U={(u1,u2,u3): u1³0, u2³0

Пример. Пусть множество U представляет собой стандартный симплекс U ={(u ₁, u ₂, u ₃): u ₁³0, u ₂³0, u ₃³0, u ₁+ u ₂+ u ₃=1} и имеется два критерия g ¹(u)=2 u ₁+7 u ₂+ u ₃ и g ²(u)=3 u ₁+ u ₂+4 u ₃.

Найдем точки максимума функции F(u)= pg ¹(u)+(1– p) g ²(u). Так как критерии в данной задаче линейны, а максимум линейной функции непременно достигается в одной из вершин, то 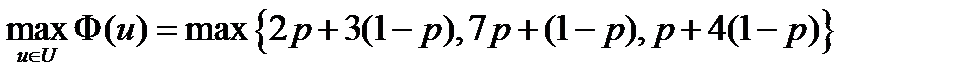. Нарисовав графики, нетрудно понять, что при 0£ p £1/3 максимум достигается в вершине (0,1,0), а при 1/3£ p £1 он достигается в вершине (0,0,1). При p =1/3 точки максимума заполняют все ребро, соединяющие эти вершины. Таким образом, все точки этого ребра являются эффективными.

Пример. Пусть множество U представляет собой стандартный симплекс U ={(u ₁, u ₂, u ₃): u ₁³0, u ₂³0, u ₃³0, u ₁+ u ₂+ u ₃=1} и имеется два критерия g ¹(u)=3 u ₁+7 u ₂+ u ₃ и g ²(u)=4 u ₁+ u ₂+4 u ₃.

Анализ, аналогичный проведенному выше, показывает, что в данном случае эффективными являются все точки, лежащие на двух ребрах: соединяющем вершину (1,0,0) с вершиной (0,1,0) и соединяющем вершины (1,0,0) и (0,0,1). В этом случае множество эффективных точек не выпукло.

В двух предыдущих примерах полезно нарисовать образ множества U в пространстве критериев.

Пример: дуополия Курно. Две фирмы выпускают однородный товар и продают его на рынке. Цена, складывающаяся на рынке, линейно убывает с ростом суммарного предложения: p=a–b (u ₁+ u ₂), где u ₁ и u ₂ объемы выпуска продукции первой и второй фирмой соответственно (по своему смыслу величины u ₁ и u ₂ неотрицательны). Пусть затраты первой и второй фирм на выпуск единицы продукции равны c ₁ и c ₂, а их цели состоят в максимизации прибылей g ¹(u ₁, u ₂)= pu ₁– c ₁ u ₁ и g ²(u ₁, u ₂)= pu ₂– c ₂ u ₂. Найдем эффективные точки в этой двухкритериальной задаче.

Для этого найдем максимум функции F(u ₁, u ₂)= p (u ₁, u ₂) +i (1– p) g ²(u ₁, u ₂)= pu ₂– c ₂ u ₂. Имеем 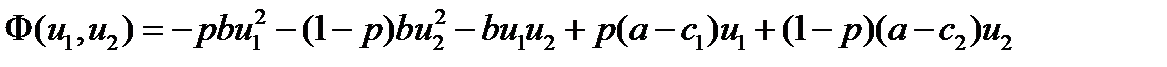. При фиксированном управлении одной фирмы эта функция представляет собой квадратный трехчлен относительно управления другой фирмы с отрицательным старшим коэффициентом. Поэтому, максимум этой функции достигается в критической точке тогда и только тогда, когда последняя лежит внутри области u ₁³0, u ₂³0. В противном случае максимум находится на границе этой области.

Критическая точка есть решение системы уравнений

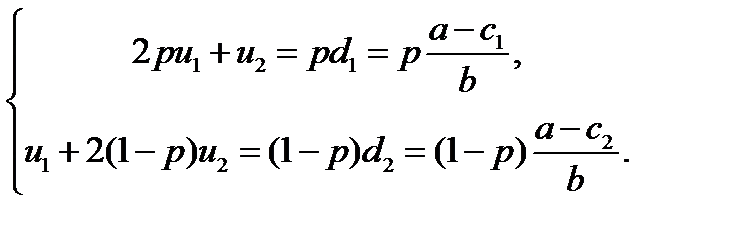
Решая эту систему относительно u ₁ и u ₂, получим параметрическое представление

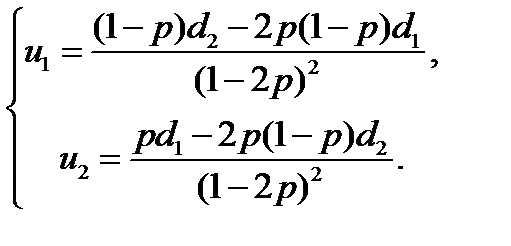
множества эффективных точек.[1]

Исключив же из этой системы параметр p, получим уравнение

2(u ₁+ u ₂)²–(d ₁+2 d ₂) u ₁–(d ₂+2 d ₁) u ₂– d ₁ d ₂=0

множества эффективных точек. Нетрудно видеть, что это уравнение параболы с осью, являющейся биссектрисой координатных углов. Пересечение этой параболы с неотрицательным квадрантом и дает множество эффективных точек[2]. Поскольку это множество пересекается с любым лучом, выходящим из начала координат и лежащим в неотрицательном квадранте, других эффективных точек н

Литература

1. Гермейер Ю.Б. Введение в теорию исследования операций. М.: Наука, 1971.
2. Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. М.: Наука, 1982.
3. Карлин С. Математические методы в теории игр, программировании и экономике. М.: Мир, 1964.