4,1. Дизъюнкция. Пусть есть m качественных критериев g 1,…, gm. Цель, состоящая в достижении, по крайней мере, одной из частных целей описывается критерием
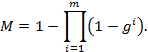
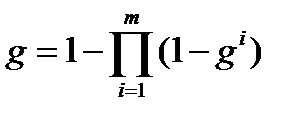 .
.
Пример. Каждый правоверный мусульманин должен хотя бы раз в жизни совершить хадж. Если годы его жизни пронумерованы числами от 1 до m и критерии g 1,…, gm описывают совершение хаджа в конкретном году, то их свертка 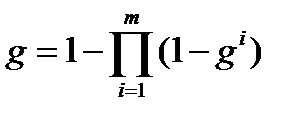 описывает выполнения этого обязательства перед Богом.
описывает выполнения этого обязательства перед Богом.
4.2. Конъюнкция. Пусть есть m качественных критериев g 1,…, gm. Цель, состоящая в достижении, сразу всех частных целей описывается критерием
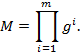
Пример. Если за сессию студенту предстоит сдать m экзаменов и каждый из критериев g 1,…, gm описывает сдачу одного из них, то цель, состоящая в успешной сдаче сессии, описывается критерием
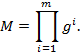
4.3. Отрицание. Пусть имеется качественный критерий g. Критерий 1– g описывает цель, состоящую в недостижении исходной, т.е, цель противоположную исходной.
Пример. Цели уменьшить риск r операции и увеличить надежность g, связаны соотношением g = 1-r
5. Обобщенное логическое свертывание колич критериев
5.1. Обобщенная дизъюнкция. Часто используется следующий способ свертки. Пусть есть m количественных критериев g 1,…, gm. Результирующий критерий образуется по правилу 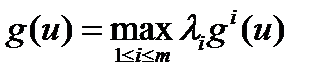 ,
, 
Пример. Пусть в шоссейной велогонке принимают участие m спортсменов из одной команды и критерии g 1,…, gm задают места, занятые ее членами. Очень часто все члены команды работают на одного лидера, то есть критерий команды есть 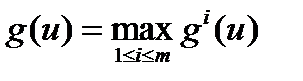 .
.
5.2. Обобщенная конъюнкция. Это свертка, при которой количественные критерии g1,…,gm заменяются общим критерием  .
.
Пример. Пусть для производства изделия требуются комплектующие m видов и количества произведенных деталей описываются числами g 1,…, gm. Критерий  описывает количество готовых изделий, которое из них можно собрать. Числа
описывает количество готовых изделий, которое из них можно собрать. Числа 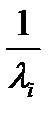 имеют при этом смысл количества деталей i -го вида, необходимых для сборки одного готового изделия.
имеют при этом смысл количества деталей i -го вида, необходимых для сборки одного готового изделия.
Заметим, что свертки (4.1), (4.2) прямо следуют из (5.1), (5.2), если все используемые функции принимают значения только 0 или 1.
5.3. Замена критерия на антагонистический. В этом случае, аналогичном случаю 4.3, максимизация критерия заменяется на минимизацию, то есть критерий g …, заменяется на M = - 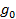
Связь 5и4-ЮБ
Пример. Инвестор анализирует целесообразность вложения средств в проект. Он рассматривает две цели: увеличение доходности и надежности 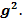 Рассмотрим различные варианты сверток.
Рассмотрим различные варианты сверток.
Экономический. Пусть потеря 1% надежности для инвестора компенсируется 5% доходности. Тогда его критерий эффективности можно записать в виде
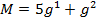
Разбиение на удовлетворительные и неудовлетворительные. Если инвестора устраивают только варианты: 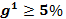 , а
, а 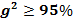 , его качественная цель запишется в виде:
, его качественная цель запишется в виде:
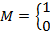
Лексикографический способ рассмотрен в примере, приведенном выше. Отметим важность ранжирования критериев. В зависимости от приоритета надежности или доходности мы получаем разные варианты вложений.
Итак, мы убедились в том, что выбор различных способов свертки приводит к различным решениям. В связи с этим появляется соблазн найти «самую хорошую» свертку, приводящую к решению эффективному с точки зрения всех анализируемых критериев.
Однако, как показал Ю.Б. Гермейер [..], эта задача принципиально не имеет решения. Более того, оказывается любая свертка может быть представлена в виде суперпозиции простых сверток, приведенных выше.
Покажем это на примере качественных целей
Теорема 1. Пусть каждый из критериев g 1,…, gm принимает лишь два значения 0 и 1, а F:{0,1} m ®{0,1} – произвольная функция. Тогда критерий M,определенный условием M (x) =F (g 1(x),…, gm (x)), может быть выражен через следующие элементарные операции:
- конъюнкция: g 1,…, gm ®
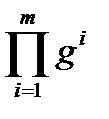
- дизъюнкция: g 1,…, gm ®

- отрицание: gi ® 1– gi.
Доказательство. Пусть v =(y 1,…, ym) – произвольный булев вектор размерности m (здесь yi равны 0 или 1 при любом i= 1,…, m). Рассмотрим функцию Fy:{0,1} m ®{0,1}, определенную условием 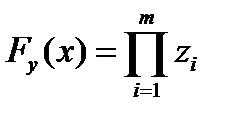 , где zi=xi, если yi =1, и zi =1– xi, если yi =0. Непосредственно проверяется, что Fy (y)=1, и Fy (x)=0 для любого x ¹ y.
, где zi=xi, если yi =1, и zi =1– xi, если yi =0. Непосредственно проверяется, что Fy (y)=1, и Fy (x)=0 для любого x ¹ y.
Для заданной нам функции F, обозначим Y ={ y: F (y)=1}. Покажем, что интересующий нас критерий g представляется в виде
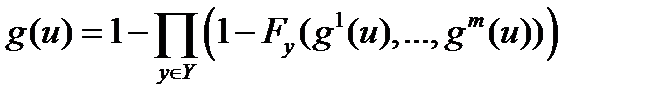 . (*)
. (*)
В самом деле, если g (u)=1, то по определению вектор t =(g 1(u),…, gm (u)) принадлежит множеству Y. Значит, произведение в формуле (*) содержит множитель
(1– FY (g 1(u),…, gm (u))), равный нулю. Следовательно, и все произведение равно нулю, а вся правая часть формулы (*) равна 1.
Если же g (u)=0, то вектор t =(g 1(u),…, gm (u)) не принадлежит множеству Y, и для всех y Î Y имеем Fy (g 1(u),…, gm (u))=0. Значит, для этого u все сомножители в формуле (*) равны 1, а тогда и произведение в правой части равенства (*) равно 1, а сама правая часть равна нулю.
Для завершения доказательства остается заметить, что при построении функций Fy мы пользовались лишь операциями отрицания и конъюнкции, а в формуле (*) использовалась еще и дизъюнкция.
Замечание. Легко видеть, что сама операция дизъюнкции может быть выражена через конъюнкцию и отрицание, то есть список «элементарных» операций может быть сокращен.
Итак, для качественных критериев показано, что любая свертка таких критериев может быть получена с помощью элементарных операций 4.1 – 4.3.
В монографии Ю.Б. Гермейера [..], показано также, что с любой точностью любая свертка произвольных критериев эффективности может быть получена суперпозицией элементарных операций вида
- экономическая свертка;
- разбиение на удовлетворительные и неудовлетворительные;
- конъюнкция(обобщенная);
- дизъюнкция (обобщенная);
- отрицание (максимизация антагонистического критерия).
Таким образом, обоснован тезис: не существует «абсолютно оптимальной» свертки. Любая свертка есть результат не формального решения о приоритетности того или иного критерия. Решение это принимает ЛПР, а консультант (исследователь операции) может формализовать это решение в виде свертки, параметры которой опять же должны быть согласованы с ЛПР.
Как правило, исследователь операции должен уметь строить множество выборов, оптимальных по Парето, а ЛПР ответственно выбирает конкретную точку из этого множества.
Определение. Будем говорить, что управление x Î X доминирует (по Парето) управление yÎX, а соответствующий вектор выигрышей (g 1(x),…, gm (x)) доминирует вектор (g 1(y),…, gm (y)), если для всех i= 1,…, m выполняются неравенства gi (x)³ gi (y), а для некоторого k выполняется строгое неравенство gk (x)> gk (y).
Определение. Будем говорить, что управление x Î X сильно доминирует (по Парето) управление yÎ X, а соответствующий вектор выигрышей (g 1(x),…, gm (x)) сильно доминирует вектор (g 1(y),…, gm (y)), если для всех i= 1,…, m выполняются неравенства gi (x)> gi (y)
Определение. Управление xÎ X, и соответствующий вектор выигрышей (g 1(x),…, gm (x)) называются эффективными (оптимальными по Парето), если не существует управления yÎX, которая доминировала бы управление x.
Определение. Управление xÎ X, и соответствующий вектор выигрышей (g 1(x),…, gm (x)) называются слабо эффективными, если не существует управления yÎX, которая сильно доминировала бы управление x.
Пусть в пространстве критериев множество выигрышей задается ломаной OABCDO.
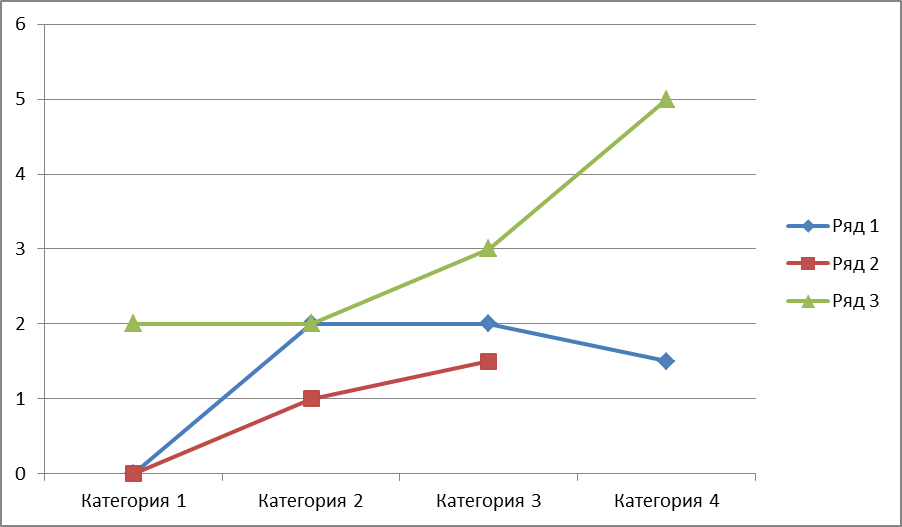
Тогда отрезок BC – определяет множество эффективных точек, отрезок AB – слабоэффективных точек.
Заметим, что для любой эффективной точки положительный ортант не содержит других точек.
Вильфредо Парето (1848-1923) – итальянский экономист.
 2015-04-01
2015-04-01 588
588








