Принцип оптимальности – это понятие определяющее
решение игры.
Решением игры является множество 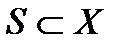 ,или
,или 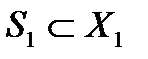 , если мы изучаем конфликт с точки зрения выделенного игрока
, если мы изучаем конфликт с точки зрения выделенного игрока 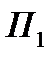 (оперирующая сторона).
(оперирующая сторона).
Пример 1. Задача оптимизации
В этом случае I= {1}- изучается поведение единственного игрока, максимизирующего свою функцию выигрыша.
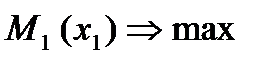
Пусть, например,
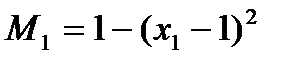
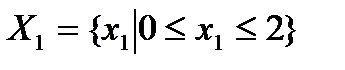
Из необходимого условия оптимальности
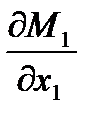 =-2(
=-2(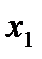 -1)=0
-1)=0
получим
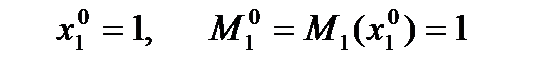 , то есть
, то есть
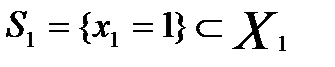
Пусть теперь функция выигрыша имеет вид:
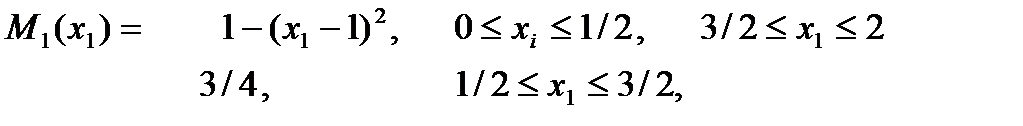
то есть прежнюю функцию мы «срезали» прямой.
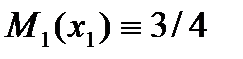 . (см. рис. 1)
. (см. рис. 1)
В этом случае, очевидно, 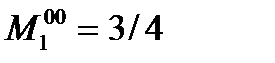 при
при 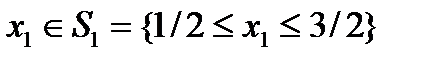
Итак,формализация принципа оптимальности и соответствующего оптимального решения в задаче оптимизации не вызывает принципиальных затруднений. Чисто технические трудности могут возникнуть при многомерных множествах 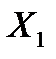 и громоздкой конструкции функции
и громоздкой конструкции функции 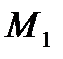 .
.
Замечание. Везде далее будет использовано обозначение Argmax 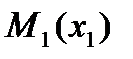 - множество точек
- множество точек 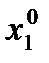 таких, что
таких, что
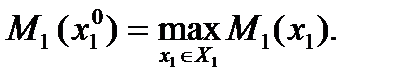
Тогда в рассматриваемом выше примере имеем:
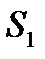 = Argmax
= Argmax 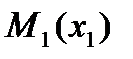
|
| ||||||||
| Х1 | ||||||||
| 0,50 | 1,50 | |||||||
| Рис.1 |
Пример2.Многокритериальная задача.
В этом случае имеем одного игрока
I={1}, но m функций, которые он желает максимизировать
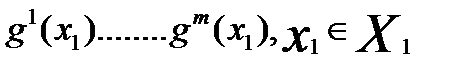
Как показано в лекции №4 для многокритериальной задачи принцип оптимальности и понятие оптимального решения определяются следующим образом. Сначала из неформальных соображений конструируется свертка критериев:
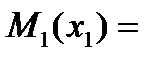 F(
F(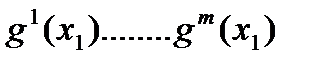 ), а затем как в предыдущем примере определяем
), а затем как в предыдущем примере определяем 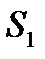 = Argmax
= Argmax 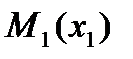 .
.
Пример. 3. Антагонистическая игра.
Антагонистическая игра-взаимодействие двух игроков с противоположными интересами.
Итак, пусть
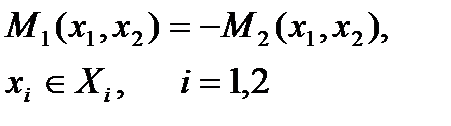
В этой игре, принципом оптимальности может служить выбор игроками седловой точки
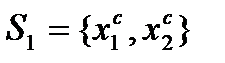 ,
,
которая по определению удовлетворяет условию
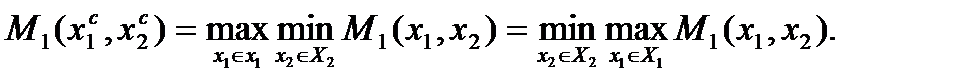
Седловая точка удовлетворяет принципу устойчивости (равновесия интересов).Если один из игроков выбрал свое управление, соответствующее седловой точке, то противнику не целесообразно отклоняться от неё.
Например, для матричной игры
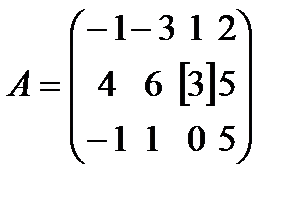 ,
,
не трудно проверить, что элемент 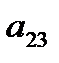 =3-наименьший во второй строке и наибольший в третьем столбце, то есть
=3-наименьший во второй строке и наибольший в третьем столбце, то есть 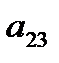 =3 соответствует седловой точке в этой игре.
=3 соответствует седловой точке в этой игре.
Если в антагонистической игре не существует седловая точка, то используются так называемые смешанные стратегии-вероятностные меры, заданные на исходных множествах управлений. В смешанных стратегиях седловая точка всегда существует, но их использование требует осторожности- осредненный выигрыш может быть не плохим, а конкретная реализация неудовлетворительной.
Пример.4. Максимально гарантированный результат(МГР)
Пусть
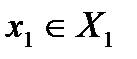 -управление игрока, а
-управление игрока, а 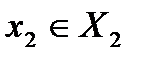 -неконтролируемые им факторы.
-неконтролируемые им факторы.
Тогда игрок гарантированно может рассчитывать на получение результата
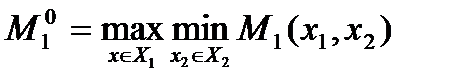
Управление 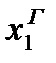 , удовлетворяющее условию
, удовлетворяющее условию
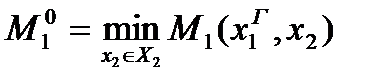 называется гарантирующим и может служить в качестве оптимального решения
называется гарантирующим и может служить в качестве оптимального решения 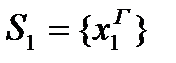 .
.
Пусть 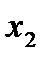 -управление партнера и игрок 1 знает его принцип оптимальности, что позволяет ему оценить его «отклик» на свое управление, то есть знать, что игрок 2 выберет
-управление партнера и игрок 1 знает его принцип оптимальности, что позволяет ему оценить его «отклик» на свое управление, то есть знать, что игрок 2 выберет 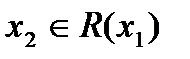 .
.
Например, если мы знаем 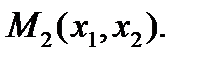 , то
, то
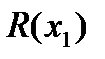 = Argmax
= Argmax 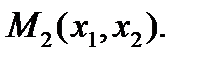
Тогда МГР игрока1 оценивается величиной
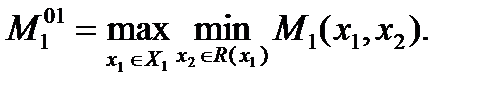
Отметим, что в следствие 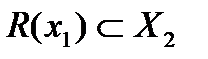 получаем неравенство
получаем неравенство 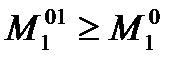 .
.
Пример.5. Бескоалиционная игра n лиц.
Эта игра общего вида
Г= 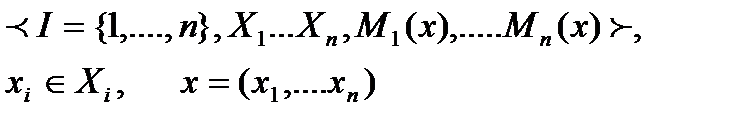
В этой модели, как и в рассматриваемой ранее модели многокритериальной задачи, решение принимается при наличии нескольких критериев. Однако эти задачи принципиально различны. В постановке многокритериальной задачи отражена нерешительность» ЛПР в оценке им критериев. Поэтому ИО может предоставить выбор ЛПР любого решения, оптимального по Парето. Выбор решения вне этого множества явно не рационален.
В случае модели конфликтной ситуации критерии «разнесены» по разным субъектам. Поэтому Парето-оптимальный выбор может быть не реализован из-за желания какого-то игрока или коалиции игроков «урвать от жизни все» - выбрать решение, увеличивающее его (их) выигрыш за счет остальных игроков.
Самым распространенным принципом оптимальности для этой игры является ситуация равновесия по Нэшу
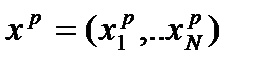 , удовлетворяющая условиям
, удовлетворяющая условиям
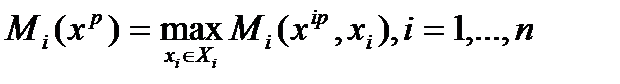
Здесь 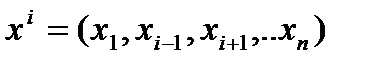
Ситуация равновесия обладает свойством устойчивости: ни одному из игроков не выгодно отклоняться от неё, если все остальные партнеры её придерживаются.
Ситуация 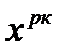 - называется ситуацией сильного равновесия, если от неё не выгодно отклоняться любой коалиции
- называется ситуацией сильного равновесия, если от неё не выгодно отклоняться любой коалиции 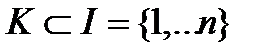
(При 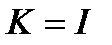 получаем ситуацию, эффективную по Парето).
получаем ситуацию, эффективную по Парето).
Как мы покажем далее, равуновесные ситуации далеко не всегда Парето-оптимальны.
Далее будем анализировать игры двух лиц и соответственно использовать запись 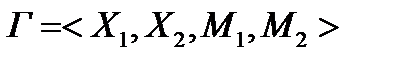 .
.
Определение: Стратегия 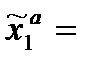
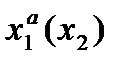 называется абсолютно оптимальной, если для любых
называется абсолютно оптимальной, если для любых 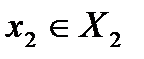 имеет место равенство:
имеет место равенство:
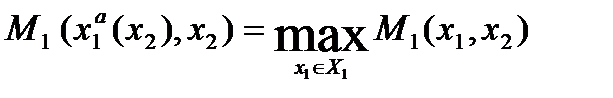
Для любого х2 первый игрок, используя такую стратегию, максимизирует свой выигрыш.
Определим x2= х2а - оптимальный ответ второго игрока из условия:
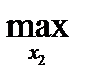 M2(x1а(x2), x2) = M2(x1а(x2а), x2а)
M2(x1а(x2), x2) = M2(x1а(x2а), x2а)
Симметрично определяется абсолютно оптимальная стратегия второго игрока.
Тогда ситуация равновесия в исходной игре определяется из условия
x1a(x2а) = x2a(x1a)
Замечание.
Прием построения абсолютно оптимальных стратегий и нахождения их пересечений для определения ситуаций равновесия носит общий характер.
Исследуем свойства ситуаций равновесия по Нэшу в следующих биматричных играх.
 2015-04-01
2015-04-01 613
613








