Методические указания к решению задач

1) Графический метод решения задач линейного программирования.

Общей задачей линейного программирования называется задача, которая заключается в определении экстремального(максимального и минимального) значения линейной целевой функции:

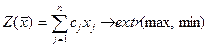, (1)

переменные 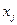, которой удовлетворяют линейным ограничениям:

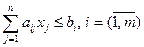(2)

и условиям неотрицательности

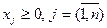(3)

где 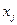- независимые переменные

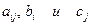- известные постоянные значения (коэффициенты и свободные члены).

Совокупность чисел 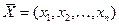, вектор которых удовлетворяют ограничениям и условиям задачи, называются допустимыми решениями(или планом). План 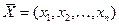при котором целевая функция (1) достигает экстремальные значения называется оптимальным.

План 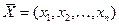основной задачи линейного программирования называется опорным, если система векторов, входящих в разложение с положительными коэффициентами 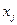линейно независима.

Так как векторы 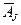являются 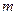- мерными, то из определения опорного плана следует, что число его положительных компонент нее превышает .

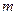Опорный план называется невырожденным, если он содержит ровно 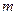положительных компонент; в противном случае план является вырожденным.

Области допустимых решений задачи линейного программирования должны быть выпуклыми множествами.

Множество точек называется выпуклым, если оно вместе с любыми двумя точками содержит их произвольную выпуклую линейную комбинацию (рис1).

Геометрический смысл этого определения состоит в том, что множеству вместе с его двумя произвольными точками полностью принадлежит и прямолинейный отрезок, соединяющий их. Примером выпуклых множеств являются: отрезок, треугольник, круг, шар, куб и т.д.(рис 1)

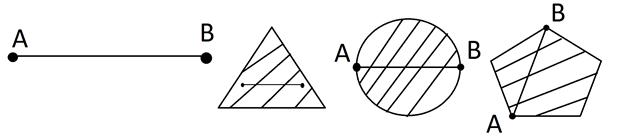
Выпуклые множества

Рис 1.

В противном случае множества называется не выпуклым (рис 2)

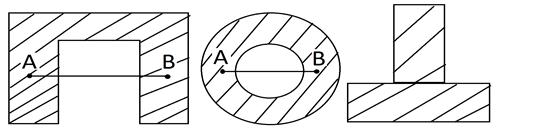
Невыпуклые множества

Рис 2

Любые 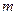переменных системы 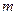линейных уравнений с 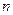переменными (при условии 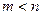) называются основными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные 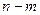переменных называются не основными.

Базисным решением системы m линейных уравнений с 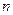переменными называется всякое ее решение, в котором все не основные переменные имеют нулевые значения.

Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с угловой точкой множества допустимых решений.

Следствие. Если оптимальное решение не единственное, то таких решений будет множество.(например, все точки отрезка, соединяющего соответствующие угловые точки)

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых значений, и наоборот.

Решение задачи линейного программирования с двумя независимыми переменными может быть выполнено графическим способом. Так как каждое из неравенств системы ограничений задачи геометрически представляют полуплоскости допустимых значений переменных с гранитными прямыми.

Если система неравенств совместна, то областью допустимых решений задачи Вляется выпуклое множество, называемое многоугольником решений. Сторонами этого многоугольника являются отрезки прямых, уравнения которых получаются из заданных ограничений заменой знаков неравенств на знаки равенств.

Последовательность решения задач линейного программирования графическим способом состоит в следующем:

1. На плоскости в координатных осях 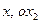строят прямые, уравнениями которых являются выражения, полученные из системы ограничений- заменой неравенств на соответствующие равенства.

2. Указываются полуплоскости, удовлетворяющие каждому из ограничений системы.

3. Строится многоугольник решений, указывая координаты вершин на нем, который называется областью допустимых решений (ОДР).

3. Транспортная задача.

Постановка задачи и ее математическая модель.

Пусть имеется однородный груз, сосредоточимый у 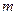поставщиков 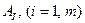в количестве 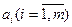единиц, который необходимо доставить 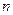потребителям 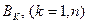в количестве 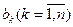единиц. Известна стоимость 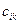перевозки единицы груза (тариф) от 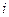-го поставщика 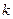-тому потребителю. Требуется составить такой план перевозок, позволяющий вывести весь груз, полностью удовлетворить заявки потребителей и имеющий минимальную стоимость.

Обозначим 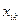количество единиц груза запланированных к перевозке от 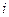-го поставщика 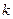-тому потребителю, тогда целевая функция имеет вид:

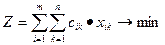, (3.1)

а ограничения можно записать следующим образом:

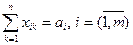, (3.2)

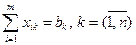. (3.3)

Необходимым и достаточным условием решения задачи (3.1)-(3.3) является уравнение баланса:

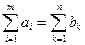(3.4)

Транспортная задача, в которой объем запасов груза и количество заявок потребителей равны, т.е. выполняется условие (3.4) называется закрытой.

Теорема 1. Любая закрытая транспортная задача имеет решение.

Условие задачи(3.1)-(3.4) обычно записывают в виде таблицы 3.1, называемой транспортной.

Таблица 3.1

Потребители B	B1	B2		Bk		Bn	Запасы
Поставщики Аi
A1	с11 х11	с12 х12	…	с1k х1k	…	с1n х1n	a1
A2	c21 х21	c22 х22	…	c2k х2k	…	c2n х2n	a2
	…	…	…	…	…	…	…
Ai	сi1 хi1	сi2 хi2	…	сik хik	…	сin хin	ai
	…	…	…	…	…	…	…
Am	сm1 хm1	cm2 хm2	…	сmk хmk	…	сmn хmn	am
Потребности	b1	b2	…	bk	…	bn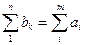

Так как транспортная задача является задачей линейного программирования, то ее решение состоит также из опорного и оптимального.

3.1. Построение опорного плана Т. З.

Теорема 2. Опорное решение закрытой модели транспортной задачи содержит 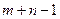базисных компонент (занятых клеток таблицы), соответствующим объемам перевозок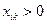

Базисными клетками транспортной таблицы являются клетки с отличными от нуля положительными перевозками, т. е. 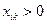. Клетки, для которых 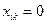называются незанятыми (свободными).

Базисные компоненты образуют опорный план (решение) транспортной задачи, если выполняются два условия:

1. сумма перевозок в каждой строке таблицы равна запасу 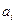в данной строке, т.е. .

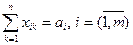2.сумма перевозок в каждом столбце равна соответствующему столбцу заявок(спроса), т.е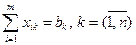

Опорный план называется вырожденным, если число нулевых перевозок (количество занятых клеток таблицы) меньше условия .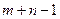

Опорный план будет невырожденным, если число нулевых перевозок, т.е. 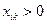, (количество занятых клеток транспортной таблицы) равно .

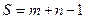При переходе от вырожденного опорного плана к невырожденному в транспортную таблицу записывают нули (обычно в клетке с наименьшей стоимостью), количество занятых клеток было равно .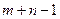

Решение транспортной задачи начинается с определения опорного плана. Для его нахождения существуют различные способы. Например, метод "северо-западного угла", способ минимальной стоимости по строке или по столбцу и минимальной стоимости всей таблицы.

Пример 3.1

Определить опорный план транспортной задачи, если три поставщика A₁, A₂ и A₃ имеют запасы однородного груза a₁=15 т, a₂=20т, a₃=30т соответственно. Весь груз требуется доставить четырем потребителям B₁, B₂, B₃ и B₄, потребности которых составляют b₁ =10 т, b₂ =16 т, b₃ =12 т и b₄ =27 т соответственно.

Матрица C тарифов имеет вид:

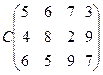
Условия задачи запишем в виде транспортной таблицы 3.2

Таблица 3.2

Потребители	B1	B2	B3	B4	Запасы груза, ai
Поставщики
A1					a1 =15
A2					a2 =20
A3					a3 =30
Потребности в грузе, bk	b1 =10	b2 =16	b3 =12	b4 =27

Рассмотрим способы построения опорного плана для транспортной задачи закрытого типа на примерах:

а) способ "северо- западного угла" (диагональный).

Таблица 3.3

Потребители	B1	B2	B3	B4	Запасы груза, ai
Поставщики
A1					a1 =15
A2					a2 =20
A3					a3 =30
Потребности в грузе, bk	b1 =10	b2 =16	b3 =12	b4 =27

Решение

Задача закрытого типа, т.к. 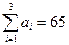и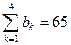

;

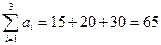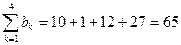
1. Заполняем таблицу 3.3 последовательно по диагонали, начиная с левой верхней клетки («северо-западный угол»).

Потребитель B₁ подал заявку на 10 единиц груза, которая удовлетворяется запасом a₁ =15 поставщика A₁. Запишем величину перевозки x₁₁=min{10;15}=10. Так как заявка потребителя B₁ удовлетворена, а запас поставщика A₁ составляет (x₁₂=a₁-b₁=15-10=5) 5 единиц груза. Удовлетворим заявку потребителя B₂ частично, так как на основании x₁₂=min{5;16}=5 и запишем значение x₁₂=5 в клетку (1,2) со стоимостью c₁₂=6 единиц.

Так как все запасы поставщика A₁ исчерпаны, то первую строку из рассмотрения исключаем.

Поскольку заявка потребителя B₂ удовлетворена не полностью, то пополнением ее запасами груза поставщика A₂, величину которого определяем из условия x₂₂=min{16-5;20}=11.

Помещаем его значение в клетку (2,2) со стоимостью перевозки c₂₂=8 единиц. Запасы потребителя B₂ удовлетворены. Доставим груз потребителю B₃ от поставщика A_2, запас которого составляет ∆a₂=a₂-x₂₂=20-11=9.

Запишем в клетку (2,3) со стоимостью c₂₃=2 величину груза из условия x₂₃=min{9;20}=9.

Так как запасы поставщика A₂ исчерпаны, то вторую строку исключаем из рассмотрения. Переходим к распределению груза поставщика A_3, т.е. рассмотрим третью строку, аналогично двум строкам таблицы.

Запишем в клетку (3,3) объем перевозимого груза от поставщика A₃ потребителю B₃ на основании условия x₃₃=min{30;12-9}=3 со стоимостью перевозки c₃₂=9 единиц.

Заключительную клетку (3,4) заполняем значением перевозимого груза за x₃₄ найденного из условия x₃₄=min{30-3;27}=27, тариф которого равен c₃₄=7.

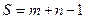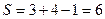
Полученное решение является опорным и невырожденным, так как условие опорности выполняется , 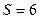занятым клеткам x₁₁=10, x₁₂=5, x₂₂=11, x₂₃=9, x₃₃=3, x₃₄=2/

Определяем стоимость перевозимого груза на основании (3.1)

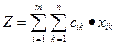
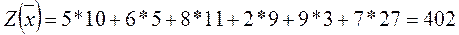
Проверка:

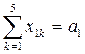10+5=15

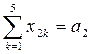11+9=20

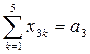3+27=30

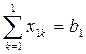10=10

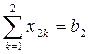5+11=16

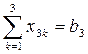9+3=12

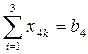3+27=30

Ответ: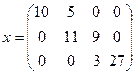

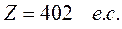
Б) способ минимальной стоимости (минимальных тарифов)

Определим опорное решение транспортной задачи способом минимальных тарифов всей таблицы. Рассмотрим решение примера 3.1.

Составим таблицу 3.4.

Таблица 3.4

Потребители	B1	B2	B3	B4	Запасы груза, ai
Поставщики
A1
A2	8
A3
Потребности в грузе, bk

Способ минимальной стоимости основан на том, что транспортируемый груз распределяется от поставщика A_i к такому потребителю B_k, стоимость перевозки к которому минимальна. В рассматриваемой задаче такой стоимостью является c₂₃=2. Помещаем в соответствующей клетке (2,3) величину груза x₂₃=min{12;20}=12. Затем размещаем груз в клетке со стоимостью c₁₄=3,величина которого равна x₁₄=min{15;27}=15.

Для стоимости c₂₁=4 величину груза определяем из условия x₁₄=min{20-12;10}=8 и поместим в клетку (2,1) таблицы 6.3. Тариф с₁₁=5 при дальнейшем распределении груза исключаем из рассмотрения, так как все запасы поставщика A₁ исчерпаны. Аналогично исключаем вторую строку. В третьей строке стоимость перевозки c₃₂=5 позволяет в клетку (3,2) записать величину груза x₃₂=min{30;16}=16. Рассмотрим клетку с тарифом с₃₁=6 в третьей строке и поместим в нее объем груза x₃₁=min{30-16;10-8}=2. Запишем в клетку (3,1) значение x₃₁=2.

Наконец в клетку (3.4) с тарифом c₃₄=7 помещаем груз x₃₄=min{30-16-2;27-15}=12.

Клетки (1,1), (1,2), (1,3), (2,2), (2,4) и (3,3) считаются не занятыми т.к. величина груза в этих клетках x_ik=0.

Условие опорности соблюдается 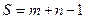, 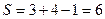. 6 занятых клеток.

Вычисляем стоимость перевозки грузов от поставщиков

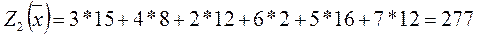
Сравнивая 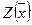и 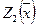видим, что Z₂<Z, следовательно, способ минимальных тарифов дает решение ближе к оптимальному.

После нахождения опорного решения транспортной задачи приступают к определению оптимального решения, т.е. нахождению минимальной стоимости перевозки грузов.