2015-04-01
610
Подмножество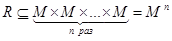 
называется n-местным отношением на множестве M.
Если (a 1, a 2,…, an)Î R, то говорят, что a 1, a 2,…, an находятся в отношении R.
Наиболее часто рассматриваются отношения при n =2 – бинарные отношения. Для записи бинарных отношений обычно используют инфиксную запись, т.е. вместо(a 1, a 2)Î R пишут a 1 Ra 2. Для сохранения бинарного отношения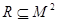 
удобно использовать матрицу 
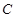размера 
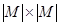. Элементы матрицы определяются следующим образом:
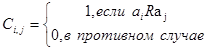
Например, отношение "меньше или равно" на множестве M={1,2,3,4} задает матрица
,
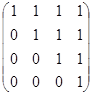отношение "меньше" на том же множестве задает матрица
,
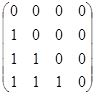отношение "иметь общий делитель не равный 1" на том же множестве задает матрица
.
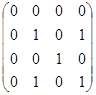Дадим определения некоторых свойств бинарных отношений.
Рефлексивность: Для всех элементов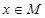 
выполняется 
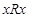, обозначение - 
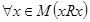. Отметим, что главная диагональ матрицы, задающей рефлексивное отношение, содержит только 1.
Антирефлексивность: Для всех элементов 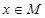не выполняется 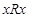, обозначение - 
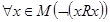. Главная диагональ матрицы, задающей антирефлексивное отношение, содержит только 0.
Симметричность: Для всех элементов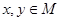 
из того, что 
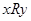следует то, что 
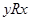, обозначение - 
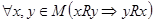. Матрица, задающая симметричное отношение, симметрична относительно главной диагонали.
Антисимметричность: Для всех элементов 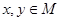из того, что 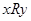и 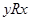следует то, что 
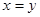, обозначение - 
.
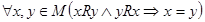Асимметричность: Для всех элементов 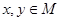из того, что 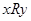следует то, что 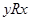не выполняется, обозначение - 
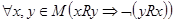. Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.
Транзитивность: Для всех элементов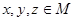 
из того, что 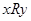и 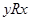следует то, что 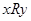, обозначение - 
.
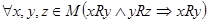Рассмотрим некоторые виды отношений.
Отношение называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Отношение называется отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно.
Отношение называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично и транзитивно.
