Общее уравнение переноса нейтронов в реакторе для плотности потока 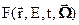 нейтронов с энергией Е, движущихся в точке r в направлении
нейтронов с энергией Е, движущихся в точке r в направлении 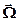 в момент времени t, можно получить исходя из требования баланса нейтронов в единичном объеме. Нейтроны, c энергией Е и скоростью
в момент времени t, можно получить исходя из требования баланса нейтронов в единичном объеме. Нейтроны, c энергией Е и скоростью 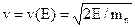 , испытывающие столкновения в этом объёме (число столкновений равно Σt(
, испытывающие столкновения в этом объёме (число столкновений равно Σt(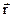 ,E)* F(
,E)* F(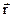 ,E,
,E, 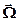 ,t)), должны были образоваться где-то на луче
,t)), должны были образоваться где-то на луче 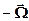 , исходящем из точки
, исходящем из точки 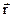 . Пусть
. Пусть 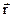 ’=
’= 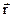 -s
-s 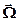 – точка на этом луче (см. рис.1). Обозначим через
– точка на этом луче (см. рис.1). Обозначим через 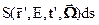 - число нейтронов интересующей нас энергии, движущихся в нужном направлении в точке r’, испускаемых в единицу времени около момента t.
- число нейтронов интересующей нас энергии, движущихся в нужном направлении в точке r’, испускаемых в единицу времени около момента t.
Число нейтронов с энергией E движущихся в направлении 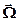 ,попадающих в рассматриваемый нами единичный объем в точке
,попадающих в рассматриваемый нами единичный объем в точке 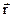 в момент времени t,определитя интегралом по лучу
в момент времени t,определитя интегралом по лучу 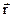 -s
-s 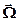 :
:
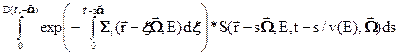
Экспоненциальный множитель определяет вероятность того, что нейтрон, рождённый в точке 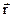 -s
-s 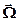 ,избежит столкновения с каким-либо ядром на пути к точке
,избежит столкновения с каким-либо ядром на пути к точке 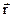 . D(
. D(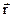 , -
, - 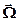 ) – расстояние до границы реактора, за которой никаких источников нейтронов уже нет. Эта граница определяется геометрией реактора.
) – расстояние до границы реактора, за которой никаких источников нейтронов уже нет. Эта граница определяется геометрией реактора.
Если в любое время t число столкновений нейтронов с энергией Е в единице объёма в точности равно числу нейтронов, попадающих в этот объём в результате прилёта из других точек пространства, лежащих в направлении – 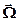 ,
,
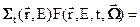
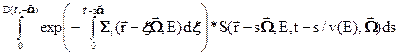 ,
,
В теории реакторов большую роль играет случай, когда плотность потока 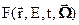 не зависит от времени. В этом случае будем говорять о стационарном уравнении переноса. Однако в общем случае оснований для постоянства потока во времени нет и если в объем влетает больше нейтронов, чем в нём сталкивается, то плотность нейтронов n= Φ /v в этом объеме будет увеличиваться, а в противном случае – уменьшаться. Из этих простых соображений получаем:
не зависит от времени. В этом случае будем говорять о стационарном уравнении переноса. Однако в общем случае оснований для постоянства потока во времени нет и если в объем влетает больше нейтронов, чем в нём сталкивается, то плотность нейтронов n= Φ /v в этом объеме будет увеличиваться, а в противном случае – уменьшаться. Из этих простых соображений получаем:
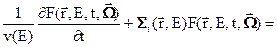
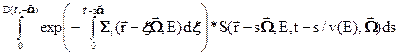 (3.1)
(3.1)
Чтобы полученное выражение было уравнением, необходимо выразить источник нейтронов 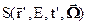 через плотность потока
через плотность потока 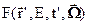 и, возможно, какие-либо другие источники, не связанные с плотностью потока нейтронов (будем называть их внешними источниками). Внешними источникам нейтронов, всегда присутствующими в реакторе, являются спонтанные деления, которым подвержены все ядра-актиниды. Вероятности спонтанного деления весьма и весьма малы, но, тем не менее, этот источник всегда присутствует. Кроме этого – естественного – внешнего источника реактор может содержать специально внедрённый в него источник нейтронов, используемый для слежения за развитием цепной реакции деления, когда реактор ещё далёк от критичности. В общем уравнении переноса нейтронов все внешние источники будем обозначать через
и, возможно, какие-либо другие источники, не связанные с плотностью потока нейтронов (будем называть их внешними источниками). Внешними источникам нейтронов, всегда присутствующими в реакторе, являются спонтанные деления, которым подвержены все ядра-актиниды. Вероятности спонтанного деления весьма и весьма малы, но, тем не менее, этот источник всегда присутствует. Кроме этого – естественного – внешнего источника реактор может содержать специально внедрённый в него источник нейтронов, используемый для слежения за развитием цепной реакции деления, когда реактор ещё далёк от критичности. В общем уравнении переноса нейтронов все внешние источники будем обозначать через 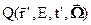 и будем считать их заданными. Как правило, внешний источник нейтронов изотропен:
и будем считать их заданными. Как правило, внешний источник нейтронов изотропен: 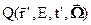 =
= 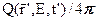 .
.
В реакторе главными процессами, обуславливающими появление в точке 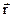 ’ нейтронов интересующей нас энергии Е, движущихся в направлении
’ нейтронов интересующей нас энергии Е, движущихся в направлении 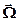 в момент времени t’ являются разного рода столкновения нейтронов. Общая плотность столкновений нейтронов в точке
в момент времени t’ являются разного рода столкновения нейтронов. Общая плотность столкновений нейтронов в точке 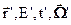 равна
равна 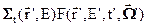 .
.
Некоторые из этих столкновений являются поглощениями и никакого вторичного источника нейтронов они не порождают.
Часть столкновений обусловлена рассеянием нейтронов на атомных ядрах. В результате рассеяния нейтрон теряет часть своей энергии[2] и меняет направление движения. Пусть Рs(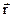 ’,E’) – вероятность рассеяния при столкновении, а
’,E’) – вероятность рассеяния при столкновении, а 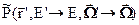 - вероятность указанного изменения энергии и направления движения нейтронов, умноженная на среднее число нейтронов, образующихся при столкновении (знак «тильда» указывает, что интеграл от
- вероятность указанного изменения энергии и направления движения нейтронов, умноженная на среднее число нейтронов, образующихся при столкновении (знак «тильда» указывает, что интеграл от 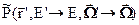 по конечным переменным может превышать единицу). Источник рассеянных нейтронов можно выразить интегралом по всем начальным направлениям и энергиям:
по конечным переменным может превышать единицу). Источник рассеянных нейтронов можно выразить интегралом по всем начальным направлениям и энергиям:
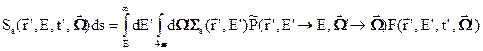 (3.2а)
(3.2а)
Здесь 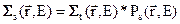
Поскольку рассматривается перенос нейтронов в реакторе, необходимо иметь в виду, что в некоторых столкновениях может происходить деление ядра. Пусть Рf(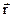 ’,E’) – вероятность деления при столкновении,
’,E’) – вероятность деления при столкновении, 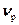 - среднее число нейтронов, мгнговенно испускаемых делящимся ядром, а
- среднее число нейтронов, мгнговенно испускаемых делящимся ядром, а 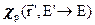 - энергетический спектр мгновенных нейтронов деления. Тогда источник мгновенных нейтронов деления может быть выражен следующим интегралом, учитывающим, что нейтроны деления испускаются изотропно (отсюда множитель 1/4π).
- энергетический спектр мгновенных нейтронов деления. Тогда источник мгновенных нейтронов деления может быть выражен следующим интегралом, учитывающим, что нейтроны деления испускаются изотропно (отсюда множитель 1/4π).
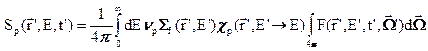 (3.2б)
(3.2б)
Здесь 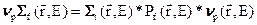 .
.
Ещё одним источником нейтронов, порождаемых при делении, являются запаздывающие нейтроны, испускаемые после бета-распадов некоторых осколков деления. Такие осколки называются предшественниками запаздывающих нейтронов. Пусть Dn(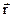 ’,t’) – концентрация ядер n-го предшественника запаздывающих нейтронов, накопившаяся к моменту t’ в точке r’,
’,t’) – концентрация ядер n-го предшественника запаздывающих нейтронов, накопившаяся к моменту t’ в точке r’, 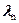 - вероятность бета-распада предшественника в единицу времени (
- вероятность бета-распада предшественника в единицу времени (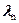 =ln2/T1/2, где T1/2 – период полураспада), рn- вероятность того, что вслед за бета-распадом произойдёт испускание нейтрона, а
=ln2/T1/2, где T1/2 – период полураспада), рn- вероятность того, что вслед за бета-распадом произойдёт испускание нейтрона, а 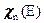 - энергетический спектр этих нейтронов. Тогда источник запаздывающих нейтронов выразится суммой по всем предшественникам:
- энергетический спектр этих нейтронов. Тогда источник запаздывающих нейтронов выразится суммой по всем предшественникам:
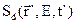 =
= 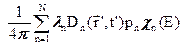 (3.2в)
(3.2в)
Концентрации 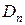 подчиняются уравнениям
подчиняются уравнениям
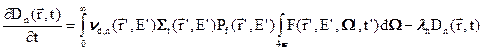 (3.3)
(3.3)
Здесь первый член описывает образование ядер предшественников типа n, испускающих при своем распаде запаздывающие нейтроны (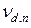 - число таких ядер, образующихся при делении); второй член описывает убыль этих ядер в результате радиоактивного распада.
- число таких ядер, образующихся при делении); второй член описывает убыль этих ядер в результате радиоактивного распада.
Теперь формулу (3.1) можно переписать в виде уравнения относительно плотности потока
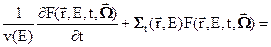
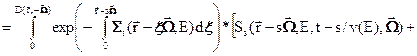 (3.4)
(3.4)
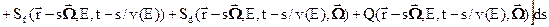 ,
,
где составляющие источника нейтронов определяются формулами (2) и (3).
Для решения уравнения (3.4) его надо снабдить граничным и начальным условиями. При расчёте реакторов обычным граничным условием является отсутствие притока нейтронов извне: в точках r на внешней границе 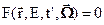 при
при 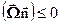 , где
, где 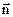 – внешняя нормаль к границе (предполагающейся выпуклой). В качестве начального условия обычно используется стационарное распределение потока нейтронов, устанавливающееся в строго критическом реакторе:
– внешняя нормаль к границе (предполагающейся выпуклой). В качестве начального условия обычно используется стационарное распределение потока нейтронов, устанавливающееся в строго критическом реакторе: 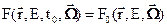 . Определение этого распределения и связанного с ним собственного числа k является первоочередной задачей нейтронного расчета реактора.
. Определение этого распределения и связанного с ним собственного числа k является первоочередной задачей нейтронного расчета реактора.
Стационарное распределение подчиняется уравнению (3.4) в котором отсутствует временная зависимость, а потому и первый член в левой части. Не нужды и в отдельном учёте запаздывающих нейтронов: из уравнения (3.3) и из здравого смысла следует, что ежесекундно в стационарном реакторе будет испускаться столько запаздывающих нейтронов, сколько образуется испускающих их ядер. Поскольку ни Sp, ни Sd от времени не зависят, эти члены можно объединить. Выражение для суммарного источника деления Sf=Sp+Sp отличается от выражения (3/2a) заменой среднего числа мгновенных нейтронов деления 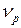 на среднее полное число испускаемых нейтронов
на среднее полное число испускаемых нейтронов 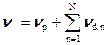 , а спектра мгновенных нейтронов деления
, а спектра мгновенных нейтронов деления 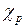 - на спектр всех нейтронов деления
- на спектр всех нейтронов деления 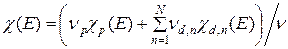 . Что касается внешнего источника, то в критическом ядерном реакторе, работающем даже на малой мощности, интенсивность испускания нейтронов деления настолько превосходит интенсивность внешнего источника, что его учётом можно пренебречь. В этом случае уравнение (4) превращается в однородное уравнение, не нулевое решение которого существует только при строго определённых условиях. Первоочередной задачей расчёта и является определение этих «определённых условий» - условий критичности. Чтобы решить эту задачу, в стационарное однородное уравнение переноса должен быть введен некий параметр, подбором которого можно было бы обеспечить существование ненулевого решения однородного уравнения. Наиболее распространённым способом введения этого параметра является деление полного числа вторичных нейтронов деления на некий коэффициент k, называемый коэффициентом размножения. В результате получаем так называемое условно-критическое уравнение в интегральной форме
. Что касается внешнего источника, то в критическом ядерном реакторе, работающем даже на малой мощности, интенсивность испускания нейтронов деления настолько превосходит интенсивность внешнего источника, что его учётом можно пренебречь. В этом случае уравнение (4) превращается в однородное уравнение, не нулевое решение которого существует только при строго определённых условиях. Первоочередной задачей расчёта и является определение этих «определённых условий» - условий критичности. Чтобы решить эту задачу, в стационарное однородное уравнение переноса должен быть введен некий параметр, подбором которого можно было бы обеспечить существование ненулевого решения однородного уравнения. Наиболее распространённым способом введения этого параметра является деление полного числа вторичных нейтронов деления на некий коэффициент k, называемый коэффициентом размножения. В результате получаем так называемое условно-критическое уравнение в интегральной форме
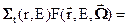
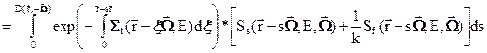 (3.5а)
(3.5а)
Если это уравнение продифференцировать по направлению 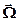 , то полечим то же уравнение в интегро-дифференциальной форме
, то полечим то же уравнение в интегро-дифференциальной форме
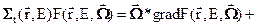
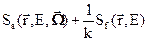 (3.5б)
(3.5б)
Уравнение должно быть дополнено граничным условием. Поскольку мы имеем дело с реактором, естественным граничным условием является равенство потока тнейтронов нулю на внешней границе реактора: нейтроны реактора целиком порождается в происходящих в реакторе деленирях. Условно-критическое уравнение заведомо имеет только тривиальное решение 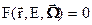 . Главный смысл решения этого уравнения в том, чтобы подобрать такое значение числа k, при котором уравнение имеет нетривиальное и всюду положительное решение. Это число является собственным числом уравнения переноса. Из теории следует, что существует множество собственных чисел, которым соответствуют ненулевые решения уравнения (3.5) при заданных граничных условиях – его собственные функции, но только одна собственная функция положительно определена при всех значениях переменных. Это решение называется главной собственной функцией, а соответствующее собственное число – главным собственным числом. Именно главное собственнное число и требуется определить.
. Главный смысл решения этого уравнения в том, чтобы подобрать такое значение числа k, при котором уравнение имеет нетривиальное и всюду положительное решение. Это число является собственным числом уравнения переноса. Из теории следует, что существует множество собственных чисел, которым соответствуют ненулевые решения уравнения (3.5) при заданных граничных условиях – его собственные функции, но только одна собственная функция положительно определена при всех значениях переменных. Это решение называется главной собственной функцией, а соответствующее собственное число – главным собственным числом. Именно главное собственнное число и требуется определить.
Следует подчеркнуть, что собственное число k введено формально и, строго говоря, лишено физического смысла. Уравнение (5) описывает стационарный нейтронный поток в реакторе только при условии, что k=1. Если расчёт показал, что собственное число отлично от единицы, то можно лишь утверждать, что если бы число нейтронов, испускаемых при делении, было бы не 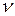 , а
, а 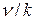 , вот тогда бы реактор был критическим. Несмотря на то, что собственное число введено формально, оно является удобной мерой отличия реактора от критического состояния и позволяет подобрать условия, при которых достигается строгая критичность. Например, если k<1, можно попытаться вывести реактор в критическое состояния путем увеличения размера активной зоны или, если это возможно, путем уменьшения концентрации поглотителя в активной зоне и т.п.
, вот тогда бы реактор был критическим. Несмотря на то, что собственное число введено формально, оно является удобной мерой отличия реактора от критического состояния и позволяет подобрать условия, при которых достигается строгая критичность. Например, если k<1, можно попытаться вывести реактор в критическое состояния путем увеличения размера активной зоны или, если это возможно, путем уменьшения концентрации поглотителя в активной зоне и т.п.
Если для реактора данной формы, состава и размеров k отлично от единицы, поток нейтронов в нём не может быть стационарен. Если в течение некоторого времени реактор был критическим и в нём сформировался стационарный поток нейтронов, а затем конструкция реактора была изменена так, что k стало меньше единицы, то поток нейтронов в реакторе будет спадать во времени. Для расчёта характера этого изменения необходимо решать нестационарное уравнение перноса (3.4) с учётом начального условия и динамики испускания запаздывающих нейтронов.
При формулировке уравнения переноса нейтронов было пренебрежено только двумя факторами. Во-первых, не учтено конечное время жизни нейтрона. Нейтрон испытывает бета-распад с периодом T1/2=10.24 мин. Поскольку время жизни нейтрона даже в реакторе на тепловых нейтронах не превышает нескольких миллисекунд, а в быстром реакторе оно намного короче, учитывать потерю нейтронов за счёт их бета-распада нет никакой нужды. Во-вторых, при формулировке уравнения не учитывалась возможность столкновения нейтронов друг с другом. Пренебрежение нейтрон-нейтронными столкновениями также вполне оправдано, если учесть, что плотность нейтронов в даже в самом высокопоточном реакторе на 10 порядков ниже плотности атомных ядер в твёрдых телах.
3.3. Макро- и микроскопические константы.
Несмотря на то, что уравнения переноса (3.4) и (3.5) достаточно сложны, современные расчётные методы позволяют их решать сколь угодно точно.
Погрешность решения в этом случае целиком определяется погрешностью коэффициентов этих уравнений – макроскопическими константами. Эти константы определяются концентрациями ядер сi(r) и микроскопическими сечениями этих ядер. Концентрации ядер в среде известного состава и плотности d вычисляются по хорошо известной формуле:
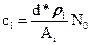 , (3.6)
, (3.6)
где 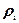 - весовая доля нуклида i, Ai – его атомный вес, N0=6.02242*1023 – число Авогадро (число молекул в грамм-моле). Под «нуклидом» здесь и далее будем понимать либо изотоп какого-либо элемента, либо природную смесь изотопов, т.е. собственно элемент.
- весовая доля нуклида i, Ai – его атомный вес, N0=6.02242*1023 – число Авогадро (число молекул в грамм-моле). Под «нуклидом» здесь и далее будем понимать либо изотоп какого-либо элемента, либо природную смесь изотопов, т.е. собственно элемент.
Что касается микроскопических сечений 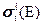 , то таковыми являются площади поперечного сечения атомных ядер. Важнейшая особенность нейтрон-ядерных взаимодействий состоит в том, что одинаковые ядра представляются нейтронам разных энергий объектами совершенно разных размеров, потому и площадь поперечного сечения ядра при нейтронных расчётах приходится считать зависящей от энергии нейтрона..
, то таковыми являются площади поперечного сечения атомных ядер. Важнейшая особенность нейтрон-ядерных взаимодействий состоит в том, что одинаковые ядра представляются нейтронам разных энергий объектами совершенно разных размеров, потому и площадь поперечного сечения ядра при нейтронных расчётах приходится считать зависящей от энергии нейтрона..
Макроскопическое полное сечение 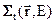 , которое было введено в предыдущем параграфе, связано с ядерными концентрациями и поперечными сечениями ядер, входящими в состав среды соотношением:
, которое было введено в предыдущем параграфе, связано с ядерными концентрациями и поперечными сечениями ядер, входящими в состав среды соотношением:
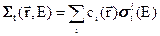 . (3.7а)
. (3.7а)
Таким образом, если мы рассмотрим слой толщиной δх, то 1 см2 этого слоя будет содержать cidx ядер нуклида i, каждое из которых имеет площадь сечения 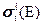 , так что
, так что 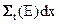 - суммарная площадь сечения всех ядер, попавших в рассматриваемый слой. Это рассуждение оправдывает применение к величине
- суммарная площадь сечения всех ядер, попавших в рассматриваемый слой. Это рассуждение оправдывает применение к величине 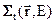 , имеющей размерность, обратную длине, название «сечение». Многие авторы трудов по теории переноса вместо
, имеющей размерность, обратную длине, название «сечение». Многие авторы трудов по теории переноса вместо 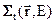 оперируют обратной величиной – средней длиной свободного пробега L(
оперируют обратной величиной – средней длиной свободного пробега L(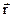 ,E). Вне зависимости от того, называть величину, обратную средней длине пробега, полным макроскопическим сечением, или нет, соотношение (3.7) связывает с экспериментально измеряемыми микроскопическими сечениями атомных ядер именно эту
,E). Вне зависимости от того, называть величину, обратную средней длине пробега, полным макроскопическим сечением, или нет, соотношение (3.7) связывает с экспериментально измеряемыми микроскопическими сечениями атомных ядер именно эту 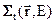 =1/L(
=1/L(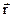 ,E). Между тем иметь представление о том, каковы длины свободного пробега нейтронов, также важно, чтобы представлять себе, через какие объекты нейтрон может пролететь не столкнувшись, а в каких он наверняка испытает множество столкновений.
,E). Между тем иметь представление о том, каковы длины свободного пробега нейтронов, также важно, чтобы представлять себе, через какие объекты нейтрон может пролететь не столкнувшись, а в каких он наверняка испытает множество столкновений.
Например, для натрия, имеющего на выходе из активной зоны температуру около 800K, плотность равна 0.845 г/см3. При молекулярном весе 23 из формулы (3.6) получаем ядерную плотность 2.2*1022 ядер в см3. Полное сечение взаимодействия быстрых нейтронов с натрием составляет, в среднем, примерно, 4 барна=4*10-24 см2. Отсюда следует, что макроскопическое сечение натрия нейтронов составляет 0.09 см-1 т.е. длина свободного пробега близка к 10 см. Поскольку заполненные натрием зазоры между тепловыделяющими элементами и между тепловыделяющими сборками существенно меньше длины свободного пробега, эти зазоры почти прозрачны для нейтронов.
Наряду с полным макроскопическим сечением можно ввести макроскопическое сечение упругого рассеяния:
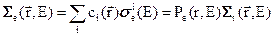 , (3.7б)
, (3.7б)
неупругого рассеяния
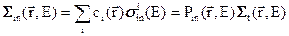 , (3.7в)
, (3.7в)
макроскопические сечения реакций (n,2n), (n,3n) и т.п.:
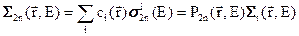 ;
;
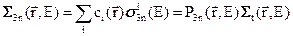 . (3.7г)
. (3.7г)
Через эти величины можно определить вероятность рассеяния, учитывающую вклады всех процессов столкновения, в результате которых появляется один или несколько вторичных нейтронов (кроме процесса деления):
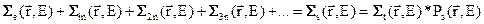 (3.8)
(3.8)
Чтобы определить макроскопическую индикатрису рассеяния 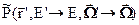 , входящую в уравнение переноса, необходимо знать индикатрисы для каждого процесса рассеяния (упругого, неупругого и др.) на каждом ядре. Эти индикатрисы зависят только от косинуса угла рассеяния
, входящую в уравнение переноса, необходимо знать индикатрисы для каждого процесса рассеяния (упругого, неупругого и др.) на каждом ядре. Эти индикатрисы зависят только от косинуса угла рассеяния 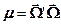 , так что
, так что
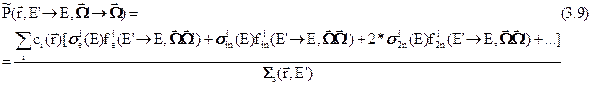 Коль скоро макроскопическая индикатриса
Коль скоро макроскопическая индикатриса 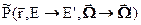 учитывает множественность нейтронов, испускаемых при рассеянии (2 в реакции (n,2n), 3 в реакции(n/3n) и т.д.), интеграл от этой функции по конечным аргументам, вообще говоря превышает единицу и она не может быть интерпретирована как вероятность (что и указывается знаком тильда).
учитывает множественность нейтронов, испускаемых при рассеянии (2 в реакции (n,2n), 3 в реакции(n/3n) и т.д.), интеграл от этой функции по конечным аргументам, вообще говоря превышает единицу и она не может быть интерпретирована как вероятность (что и указывается знаком тильда).
Все процессы, обобщённые под словом «рассеяние» отличаются тем, что образованные в них нейтроны имеют энергию, меньшую, чем нейтрон до рассеяния. Энергетический спектр нейтронов, образующихся при делении, 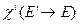 довольно слабо зависит от энергии нейтронов, вызывающих деление и поэтому последний интеграл по энергии в уравнении (3.5) берётся по всем возможным энергиям. Макроскопические характеристики среды, входящие в этот интеграл, выражаются через микроскопические характеристики делящихся ядер – сечение сечение деления
довольно слабо зависит от энергии нейтронов, вызывающих деление и поэтому последний интеграл по энергии в уравнении (3.5) берётся по всем возможным энергиям. Макроскопические характеристики среды, входящие в этот интеграл, выражаются через микроскопические характеристики делящихся ядер – сечение сечение деления 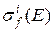 , среднее число нейтронов, испускаемых при делении
, среднее число нейтронов, испускаемых при делении 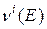 и спектр нейтронов деления
и спектр нейтронов деления 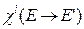 – следующим образом:
– следующим образом:
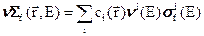 . (3.10)
. (3.10)

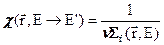
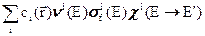 . (3.11)
. (3.11)
При решении нестационарного уравнения (3.4) требуется знать число как мгновенных 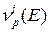 , так и всех запаздывающих
, так и всех запаздывающих 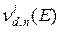 нейтронов деления и, соответственно, их спектры
нейтронов деления и, соответственно, их спектры 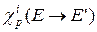 и
и 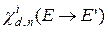 .
.
Пространственная зависимость ядерных концентраций (а потому и макроконстант), как правило, кусочно-постоянна. Исключение составляют случаи, когда требуется учитывать изменение нуклидного состава в процессе выгорания, в результате которого состав топливного (или поглощающего) стержня оказывается зависящим от координат. Путем разбиения первоначально однородных материальных зон на части и эта задача сводится к случаю кусочно-постоянных сечений.
Что касается энергетических зависимостей нейтронных сечений и энерго-угловых распределений рассеянных нейтронов, то они чрезвычайно сложны и многообразны и учёт этих зависимостей является фактором, весьма затрудняющим решение уравнения переноса. Характер этих зависимостей и источники данных о нейтронных сечениях будут рассмотрены ниже.
 2015-04-06
2015-04-06 5363
5363








