Момент инерции плоской треугольной пластины относительно оси, проходящей через центр масс перпендикулярно ее плоскости

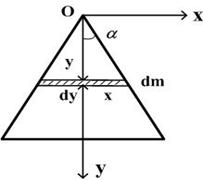
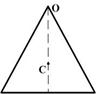
Разобьем пластину на тонкие стержни массой dm длиной 2 x и высотой dy, как показано на рисунке. Так как для стержня длины 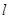момент инерции относительно перпендикулярной оси, проходящей через центр масс равен 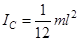, то момент инерции такого стержня относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, по теореме Штейнера, равен:

,

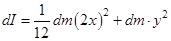где массу стержня 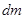можно выразить из пропорции

,

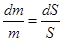где 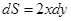– площадь стержня, а 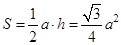– площадь равностороннего треугольника.

Тогда масса стержня: 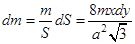, а его момент инерции: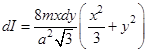

С учетом того, что для равностороннего треугольника 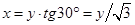, получим: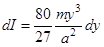

Тогда 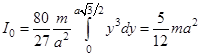. Но по теореме Штейнера 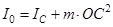, тогда, учитывая, что 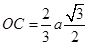, получим выражение для :

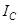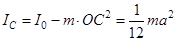
Контрольные вопросы

1. В чем заключается физический смысл момента инерции?

2. От чего зависит момент инерции?

3. Сформулируйте теорему Штейнера.

4. С помощью теоремы Штейнера объясните, относительно какой оси момент инерции тела минимален (максимален)?

5. Получите расчетную формулу для момента инерции плоской прямоугольной пластины относительно оси, проходящей через центр масс, и лежащей в плоскости пластины.

6. Получите расчетную формулу для момента инерции пластины в форме равностороннего треугольника относительно оси, лежащей в плоскости пластины и проходящей через одну из его сторон.

7. Как нужно проводить эксперимент в данной работе, чтобы расчетные формулы, которыми вы пользовались, были справедливы

Лабораторная работа №7