2015-04-06
1398
При условии малых колебаний, т.е.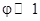 
рад, колебания диска можно считать гармоническими с периодом 
:
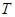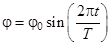(1)
Пусть диск поднялся на максимальную высоту
.
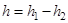Тогда приращение потенциальной энергии равно:
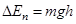
При последующем вращении диска потенциальная энергия переходит в кинетическую энергию вращательного движения
,
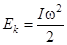где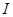 
– момент инерции тела относительно оси вращения, w – угловая скорость вращения.
В момент прохождения положения равновесия кинетическая энергия принимает максимальное значение, и, пренебрегая трением, можно записать закон сохранения энергии:
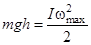. (2)
Угловую скорость диска можно найти, взяв производную от j из (1):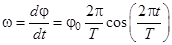 
тогда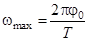 
. (3)
Величину h можно найти, считая, что при повороте диска на малый угол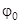 
можно приблизительно считать, что 
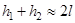. Тогда
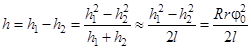, (4)
где учтено, что (см. рис.1)
, 
, 
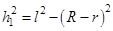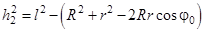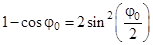, а также, что вследствие малости угла 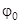, синус можно заменить значением самого угла в радианах.
В результате подстановки (4) и (3) в (2), получим расчётную формулу для момента инерции маятника массой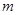 
:
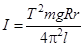(5)
|
|
|
По зависимости (5) можно рассчитать момент инерции как нагруженного исследуемой пластиной, так и ненагруженного диска В. Тогда, вследствие аддитивности, момент инерции исследуемого тела (пластины) легко определяется по формуле:
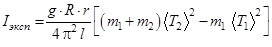(6)
где 
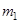и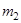 
– массы ненагруженного диска и исследуемой пластины соответственно, а 
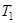и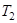 
– период колебаний ненагруженного и нагруженного диска соответственно.
Момент инерции есть мера инертности тела при его вращательном движении. Это значит, что чем больше момент инерции, тем больший момент сил необходимо приложить к телу, чтобы заставить тело вращаться, если оно покоилось, или остановить, если вращалось.
Момент инерции материальной точки: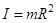 
, где 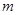– масса точки, а R – расстояние от нее до оси вращения. Момент инерции– величина аддитивная, т.е. момент инерции системы материальных точек или твердого тела определяется как сумма моментов инерции частей, из которых состоит система или тело, т.е. 
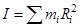или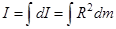 
(*)
Момент инерции зависит от формы и размеров тела или системы, а также от положения и ориентации в пространстве оси, относительно которой определяется момент инерции.
Например, если известен момент инерции тела относительно оси, проходящей через его центр масс, то относительно любой другой оси его можно рассчитать с помощью теоремы Штейнера: момент инерции тела относительно произвольной оси О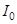 
равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс С 
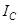, и произведения массы тела на квадрат расстояния между осями (ОС = d), т.е.
IО = IС + m d2.
Моменты инерции тел относительно оси, проходящей через центр масс IС можно определить, пользуясь определением (*) и разбивая тело на элементы
|
|
|
