Возникновение и развитие теории вероятностей как науки

Еще первобытный вождь понимал, что у десятка охотников «вероятность» поразить копьем зубра гораздо больше, чем у одного. Поэтому и охотились тогда коллективно.

Неосновательно было бы думать, что такие древние полковод­цы, как Александр Македонский или Дмитрий Донской, готовясь к сражению, уповали только на доблесть и искусство воинов.

Несомненно, они на основании наблюдений и опыта военного руководства умели как-то оценить «вероятность» своего возвращения «со щитом» или «на щите», знали, когда принимать бой, когда уклониться от него. Но они были еще очень далеки от теории вероятностей.

Позднее, с опытом, человек все чаще стал планировать случай­ные события – наблюдения и опыты, классифицировать их исхо­ды как невозможные, возможные и достоверные. Он заметил, что случайностями не так уж редко управляют объективные закономер­ности. Вот простейший опыт – подбрасывают монету. Выпадение герба или цифры, конечно, чисто случайное явление. Но при много­кратном подбрасывании обычной монеты можно заметить, что появление герба происходит примерно в половине случаев. Значит, результаты бросаний монеты, хотя каждое из них и явля­ется случайным событием, при неоднократном повторении подвласт­ны объективному закону. Для тех, кто обладает склонностью к ис­следованиям, появляется соблазн накопить побольше таких законо­мерностей и попытаться построить из них теорию.

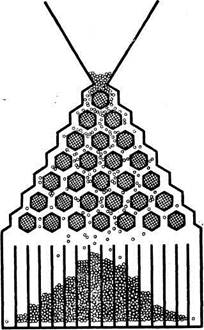
Рис. 6

Рассмотрим другой, более сложный пример — эксперимент с так называемой доской Гальтона (рис. 6). Доска размещена вер­тикально. Из верхнего резервуара стальные шарики катятся (на отдельных участках падают) вниз и накапливаются в нижних гнездах.

Каждый шарик, встретив на своем пути очередное препят­ствие, отклоняется или влево или вправо, а затем падает вниз. Шарик, конечно, может попасть в любое из гнезд.

Между тем правильное расположение шариков (симметричное, при котором в центральных гнездах их много, а в крайних мало), повторяющееся от экс­перимента к эксперименту, убе­дительно свидетельствует о су­ществовании объективного за­кона их распределения. Когда шариков много, то говорят, что они распределены по нормаль­ному закону.

Итак, случайности могут под­чиняться относительно простым и более сложным закономернос­тям. Но, спрашивается, где же математика, где математические задачи?

Наиболее интересные для на­чинающих задачи теории вероят­ностей возникли в области азарт­ных игр, хотя формированию основ теории вероятностей спо­собствовали также выяснение длительности жизни, подсчет населения, практика страхова­ния. К азартным играм относили бросание шестигранных играль­ных костей.[1] На­пример, при бросании двух кос­тей трудным («азар») считалось появление в сумме двух или две­надцати очков.

В 1494 году итальянский математик Л. Пачоли (1445–1514) опубликовал энциклопедический труд по математике, в котором разбирал проблему справедливого разделения ставки. Сам Пачоли верного решения не нашел. Он предлагал разде­лить ставку, не учитывая числа партий, которые нужно еще выиграть, чтобы получить всю ставку.

Спустя без малого пятьдесят лет, другой итальянский математик Д. Кардано (1501–1576) подверг рассуждения Пачоли справедли­вой критике, но и сам предложил ошибочное решение.

Прошло еще 100 с лишним лет, и в 1654 году задача была, на­конец, решена в ходе переписки между двумя выдающимися фран­цузскими математиками Б. Паскалем (1623–1662) и П. Ферма (1601–1665).

В 1718 году в Лондоне вышла в свет книга со странным по тем временам названием «Учение о случаях». Ее автор – французский математик А. Муавр (1667–1754). Самое большое его достижение – открытие закономерности, которая очень часто наблюдается в слу­чайных явлениях. Он первым заметил и теоретически обосновал роль «нормального» распределения (вспомните опыт Гальтона). Закон нормального распределения имеет важное практическое значение. Оказывается, что так распределяется скорость газовых молекул, вес новорожденных и много других случайных событий физической и биологической природы.

Впервые основы теории вероятностей были изложены последо­вательно французским математиком П. Лапласом (1749–1827) в книге «Аналитическая теория вероятностей».

П. Лаплас не мог предусмотреть, что пройдет несколько десяти­летий и интерес к теории вероятностей снизится. А так на деле и случилось. Во второй половине XIX века и в начале XX века неко­торые математики перестали интересоваться теорией вероятностей как математической дисциплиной.

Чем объясняется такое безразличие некоторых математиков к теории вероятностей? Причин много. Но здесь мы раскроем только одну.

Вероятность события была определена Лапласом так:

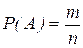, (1.3)

где п – общее число равновозможных событий, a m – число тех событий, когда происходит нужный исход («благоприятствующее событие»).

Кажется, что все в порядке – к лапласовскому определению вероятности события никак не придраться. Но вот вопрос: когда и какие случайные события можно считать равновозможными?

Рождается ребенок. Мальчик или девочка – кажется, равновозможные события (одно из двух, как и при бросании монеты). Но оказывается, что статистика рождений не вполне согласуется с нашим «кажется».

Она может быть, например, такой:

	Год	Число родив­шихся детей	Число родив­шихся мальчиков	Число родив­шихся девочек	Частота рождения мальчиков
Польша Швеция	1927 1935	958 733 88 273	496 544 45 682	462189 42 591	0,518 0,517

Если в разное время в разных странах мальчиков рождается больше, чем девочек, значит, вероятности рождения мальчика или девочки неодинаковые: вероятность события «родился мальчик» больше .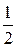

Вспомним о подбрасывании монеты (см. об этом выше). Откуда у нас уверенность, что вероятность выпадения герба, когда подбрасывание неограниченно повторяется, равна ?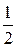

Факты, обнаруживающие, что объективная реальность не обязательно совпадает с человеческим «кажется», послужили причиной сомнений в правомерности понятия «равновозможные события». Возникла потребность «перепроверять» вероятности, которые вы­числялись по лапласовской формуле 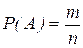, экспериментами.

Противоречия, которые проявились при оценке вероятности некоторого события и частоты того же события не могли понравиться многим математикам, которыезаботи­лись о строгости науки. Вместе с тем распространению «антивероятностных» взглядов способствовало опубликование ряда парадоксов. Один из наиболее характерных парадоксов – парадокс Бертрана.

Стойко защищали позиции теории вероятностей русские мате­матики. В 1846 году Петербургская Академия наук издала книгу В. Я. Буняковского (1804–1889) под названием «Основания мате­матической теории вероятностей». Это был первый русский учебник по теории вероятностей. По нему учился и выдающийся русский ма­тематик П. Л. Чебышев. Хотя он по теории вероятностей написал не так уж много трудов, но все они сохраняют первостепенное зна­чение вплоть до наших дней. Так называемое неравенство П. Л. Чебышева на веки веков вошло в сокровищницу математической науки.

Ученик П. Л. Чебышева А. А. Марков развил труды своего учи­теля. Ему принадлежит слава открывателя важной области применения теории вероятностей – теории вероятностных, или стохастических, процессов.

Наследие русских математиков получило развитие в работах советских математиков Е.Е. Слуцкого, С.Н. Бернштейна, А.Я. Хинчина, Ю.В. Линника и особенно академика А.Н. Колмогорова. Созданная А.Н. Колмогоровым советская школа теории вероятностей завоевала всеобщее признание и сегодня занимает ведущие позиции в мировой науке.