2015-04-06
225
Пример. Исследовать функцию 
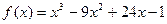
и построить её график.
Решение. Исследование свойств данной функции проводится по схеме, приведенной в учебнике Валуцэ И.И. «Математика для техникумов» на стр.233.
Функция f(x) является непрерывной и дифференцируемой на всей числовой прямой.
Так как f(1)=15 и f(-1)=-35, то функция f(x) не является ни четной, ни нечетной. Кроме того, как функция f(x) принимает значение 0 не более чем в трех точках, то она не является периодической.
Из соотношений
, 
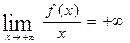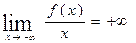
следует, что ни горизонтальных, ни наклонных асимптот график функции y=f(x) не имеет.
Найдем промежутки, на которых функция f(x) монотонная. Так как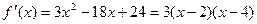 
, то а) 
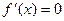при x=2 и x=4, б) 
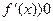при х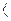 
2 или х 
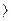4, в) 
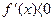при 2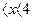 
. Следовательно, функция f(x) возрастает на промежутках 
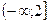и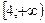 
и убывает на промежутке 
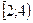. Точка х=2 является точкой локального максимума функции f(x) (f(2)=19), а точка х=4 – точкой её локального минимума (f(4)=15).
Для того чтобы найти промежутки выпуклости данной функции, нужно найти участки возрастания и убывания функции
.
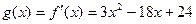Так как функция g(x) – Квадратный трехчлен с положительным коэффициентом при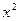 
, то она убывает на промежутке 
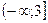и возрастает на промежутке 
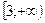. Отсюда заключаем, что функция f(x) является выпуклой вверх на промежутке 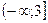и выпуклой вниз на промежутке .
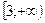| x |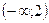 
| 
| 
| 
| |||
| + | - | - | - | + | ||
| - | - | - | + | + | + | |
| 
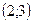
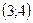
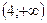
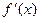
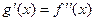
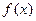
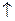
| max |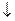 
| точка пере- гиба |
| min |
|
Результаты проведенного исследования функции f(x) приведены в таблице, по которой строится график.
