1) по возможности таблицу следует составлять небольшой по размеру, легко обозримой. Иногда целесообразно вместо одной большой таблицы построить несколько органически связанных между собой, последовательно расположенных таблиц.
2) Общий заголовок таблицы должен кратко выражать её основное содержание. В нём обыкновенно указываются время, территория, к которым относятся данные, единица измерения, если она выступает единой для всей совокупности. При отсутствии общей единицы измерения в каждой графе проставляется своя единица измерения.
3) Обыкновенно строки подлежащего и графы сказуемого располагают в виде частных слагаемых с последующим подытоживанием по каждому из них. При неполном объёме данных все слагаемые сначала показываются в строке «общие итоги», а потом после пояснения в стоке «в том числе» перечисляют наиболее важные их составные части.
4) Для удобства анализа таблицы при большом числе строк подлежащего и граф сказуемого возникает потребность в нумерации тех из них, которые заполнены данными. Подлежащие и единицы измерения обыкновенно обозначаются буквами (А, Б, В и т.д.).
5) При заполнении таблиц следует использовать следующие условные обозначения: при отсутствии явления пишется прочерк «—», если нет информации о явлении, ставится многоточие «…» или пишется «нет сведений». Если изучаемое значение признака не имеет осмысленного содержания, то ставится «Х».
6) Одинаковая степень точности обязательна для всех чисел, что обеспечивается соблюдением правил их округления (от 0,1 до 0,01).
7) Когда в таблице проводятся наряду с отчётными данными сведения расчётного порядка, об этом следует сделать соответствующую оговорку.
Сттистические графики представляют собой условные изображения числовых величин и их соотношений посредством линий, геометрических фигур, рисунков или карт-схем.
Графический способ облегчает рассмотрение статистических данных, делает их наглядными, выразительными, обозримыми. На графике видны пределы изменения разных показателей, их колеблемость, сравнительная скорость изменения различных показателей, их вариация. Но вместе с тем графики имеют определённые ограничения: график не может включить столько данных как таблица, на графике показываются всегда округлённые данные. ТО график используется для изображения общей ситуации, а не деталей.
В ст. графике различают следующие основные элементы:
1) поле графика – место, на котором он выполняется. Поле графика характеризуется его форматом (размером и пропорциями сторон). Принято считать, что наиболее оптимальным для зрительного восприятия является график, выполненный на поле прямоугольной формы с соотношением сторон от 1:1,3 до 1:1,5 (правило «золотого сечения»).
2) Графический образ – символические знаки, с помощью которых изображаются ст. данные (линии, точки, геометрические фигуры). Графический образ должен наглядно отображать изучаемые показатели и соответствовать основному предназначению графика.
3) Пространственные ориентиры — определяют размещение графических образов на поле графика. Они задаются координатной сеткой или контурными линиями и делят поле графика на части, соответствующие значениям изучаемых показателей.
4) Масштаб графика — мера перевода численной величины в графическую.
5) Масштабная шкала — линия, отдельные точки которой читаются как определённые числа. В масштабной шкале различают: линию – носитель информации, являющуюся опорой шкалы, помеченные на ней чёрточками точки, цифровые обозначения чисел, соответствующие определённым точкам.
6) Экспликация графика — пояснение его содержания, включает в себя заголовок графика, объяснения его масштабных шкал, пояснения отдельных элементов графического образа.
7) Заголовок графика — в краткой и чёткой форме поясняет основное содержание изображаемых данных.
По способу построения ст. графики подразделяются на диаграммы, картодиаграммы и картограммы.
Диаграмма – чертёж, на котором ст. информация изображается посредством геометрических фигур или символических знаков.
Наибольшее распространение получили линейные диаграммы.
Ленточные диаграммы
Круговые диаграммы
фигурные диаграммы
картограмма – схематическая карта, или план местности, на которой отдельные территории в зависимости от величины изображаемого показателя обозначаются с помощью графических символов (штриховки, расцветки, точек).
Картодиаграмма – сочетание контурной карты (плана местности) с диаграммой. В отличие от диаграммы используемые геометрические символы располагаются не в один ряд, а по всей карте.
Тема 4. Средние величины в статистике: Значение и сущность средних величин. Основные виды средних величин. Свойства средней арифметической. Мода и медиана. Квартили и децили.
Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.
Объективность и типичность статистической средней обеспечивается при следующих условиях:
1. Средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок.
2. Для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц, колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.
При использовании средних в практической работе и научных исследованиях необходимо иметь в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности.
Среднюю величину часто называют показателем центра исследуемых данных или показателем центральной тенденции.
Расчет средней величины включает две операции: суммирование данных по всем единицам (обобщение данных) и деление на число единиц (приведение обобщенной характеристики к единице совокупности).
Средняя обозначается как 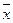 . Такой способ обозначения указывает на происхождение средней из конкретных величин. Черта вверху символизирует процесс осреднения индивидуальных значений.
. Такой способ обозначения указывает на происхождение средней из конкретных величин. Черта вверху символизирует процесс осреднения индивидуальных значений.
Частота – повторяемость индивидуальных значений признака, обозначается буквой f.
Частости – удельные веса или доли, относительные величины, обозначаются w.
В экономических исследованиях и плановых расчетах преимущественно применяются следующие виды средних:
1. Средняя арифметическая. Широко применяется в плановых расчетах при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок.
Простая средняя: Взвешенная:
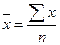 ,
, 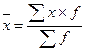
где x – значение признака единицы совокупности,
п – количество единиц совокупности,
f – частота.
2. Средняя гармоническая. Величина, обратная средней арифметической из величин, обратных данным. В качестве весов используются частости.
Простая средняя: Взвешенная:
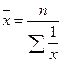
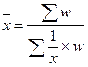
3. Средняяквадратическая. Используется для расчета среднего квадратического отклонения – основного показателя вариации.
Простая средняя: Взвешенная:
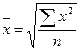
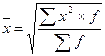
4. Средняя геометрическая. Используется при вычислении среднего коэффициента роста (темпа) в рядах динамики.
Простая средняя: Взвешенная:
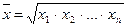
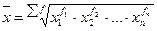
Полученные значения разных средних из одних и тех же чисел можно проранжировать (упорядочить) следующим образом:
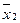 >
> 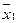 >
> 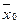 >
> 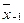
то есть средние ранжируются по показателю степени k. Соотношение форм средних, выраженное в виде данного неравенства, называется свойством мажорантности средних.
Основной формой средних является средняя арифметическая. Ее формула прямо отвечает определению средней величины как обобщенной характеристики единицы совокупности. Рассмотрим свойства средней арифметической:
1. 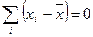 - сумма отклонений от средней равна нулю. Поэтому среднюю можно назвать центром распределения данных: значения ниже и выше средней величины взаимно уравновешиваются.
- сумма отклонений от средней равна нулю. Поэтому среднюю можно назвать центром распределения данных: значения ниже и выше средней величины взаимно уравновешиваются.
2. 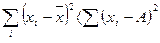 - сумма квадратов отклонений от средней арифметической меньше суммы квадратов отклонений от произвольно выбранного числа А.
- сумма квадратов отклонений от средней арифметической меньше суммы квадратов отклонений от произвольно выбранного числа А.
3. 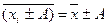 - если каждую варианту xi увеличить или уменьшить на величину А, то средняя увеличится или уменьшится на ту же величину А.
- если каждую варианту xi увеличить или уменьшить на величину А, то средняя увеличится или уменьшится на ту же величину А.
4. 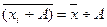 - если каждую варианту xi уменьшить в А раз, то средняя уменьшится в А раз.
- если каждую варианту xi уменьшить в А раз, то средняя уменьшится в А раз.
5. 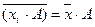 - если каждую варианту xi увеличить в А раз, то средняя увеличится в А раз.
- если каждую варианту xi увеличить в А раз, то средняя увеличится в А раз.
6. 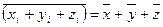 - средняя многочлена равна многочлену средних.
- средняя многочлена равна многочлену средних.
7. 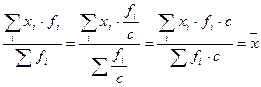 - если, используя взвешенную среднюю, увеличить или уменьшить все веса в с раз, то средняя не изменится.
- если, используя взвешенную среднюю, увеличить или уменьшить все веса в с раз, то средняя не изменится.
Мода и медиана относятся к структурным средним, которые выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач.
Модой называют значение признака, которое наиболее часто встречается в совокупности.
В дискретном ряду модой является вариант с наибольшей частотой (частостью).
В интервальном вариационном ряду мода рассчитывается по формуле:
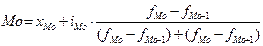
где xMo – нижняя граница модального интервала;
iMo - величина модального интервала;
fMo, fMo-1, fMo+1 - частоты (частости) соответственно модального, домодального (предмодального) и послемодального интервалов.
Модальный интервал – это интервал, имеющий наибольшую частоту (частость).
Приближенно модальное значение признака можно определить графически – по гистограмме. Для этого нужно взять столбец, имеющий наибольшую высоту, и из его левого верхнего угла провести отрезок в верхний угол последующего столбца, а из правого угла – провести отрезок в верхний правый угол предыдущего. Абсцисса точки пересечения отрезков и будет соответствовать модальному значению признака в изучаемой совокупности.
Медиана – значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.
Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания значений признака.
В дискретном ряду распределения ля определения медианы сначала определяют ее место в ряду, используя формулу:
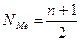 ,
,
где п – число членов ряда.
Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую из двух серединных значений.
В интервальном ряду распределения сначала указывают интервал, в котором находится медиана. Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений. Численное значение медианы определяется по формуле:
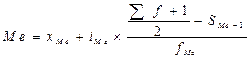
где xMе – нижняя граница медианного интервала;
iMе – величина медианного интервала;
fMе – частота (частость) медианного интервала;
S Me-1 – накопленная частота интервала, предшествующего медианному.
Медиану приближенно можно определить графически по кумуляте. Для этого высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной.
Квартили и децили относят к структурным средним.
Квартиль – значения признака, которые делят ранжированный ряд на четыре равные по численности части. Таких величин будет три. Вторая квартиль является медианной.
Место квартили определяется следующим образом:
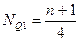 ;
; 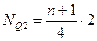 ;
; 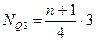
Затем по накопленным частотам в дискретном ряду определяют численное значение.
В интервальном ряду распределения сначала указывают интервал, в котором лежит квартиль, затем определяют ее численное значение по формуле:
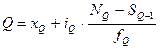 ,
,
где xQ – нижняя граница интервала, в котором находится квартиль;
SQ-1 – накопленная частота интервала, предшествующего тому, в котором находится квартиль;
fQ – частота интервала, в котором находится квартиль.
Децили широко применяются в анализе дифференциации различных социально-экономических явлений.
Децили – значения признака, которые делят ранжированный ряд на десять равные по численности части. Таких величин будет девять. Место децилей определяется по формуле:
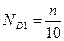 ;
; 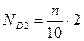 ;…
;… 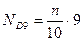 .
.
Для интервального ряда децили определяются следующим образом:
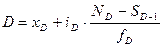 ,
,
где xD – нижняя граница интервала, в котором находится дециль;
SD-1 - накопленная частота интервала, предшествующая тому, в котором находится дециль;
fD - частота интервала, в котором находится дециль.
Тема 5. Показатели вариации: Понятие вариации. Абсолютные показатели вариации. Дисперсия и её свойства. Относительные показатели вариации. Общая дисперсия, групповая и межгрупповая.
Вариацией называют различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени. Она возникает в результате того, что индивидуальные значения складываются под совместным влиянием разнообразных условий (факторов), по-разному сочетающихся в каждом отдельном случае.
Случайная вариация – вариация, которая не зависит от факторов, положенных в основу выделения групп.
Изучение вариации в пределах однородной группы предполагает выполнение следующих этапов:
· построение вариационного ряда;
· графическое изображение вариационного ряда;
· исчисление основных характеристик распределения.
Вариационный ряд – групповая таблица, построенная по количественному признаку, в сказуемом которой показывается число единиц в каждой группе.
Форма построения вариационного ряда зависит от характера изменения изучаемого признака. По характеру вариации значений признака различают:
· признаки с прерывным изменением (дискретные);
· признаки с непрерывным изменением (непрерывные).
Для признака, имеющего прерывное изменение и принимающего небольшое количество значений, применяется построение дискретного ряда. В первой графе ряда указываются конкретные значения каждого индивидуального значения признака, во второй графе численность единиц с определенным значением признака.
Для признака имеющего непрерывное значение, строится интервальный вариационный ряд. В первой графе отдельные значения признака указываются в интервалах «от – до», во второй графе – число единиц, входящих в интервал. Интервалы образуются равные и закрытые.
Величина интервала определяется по формуле:
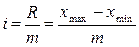
где R - размах колебания (варьирования) признака;
m - число групп.
Число групп приближенно определяется по формуле Стерджесса:
m = 1+3.322 lg n,
где n – число единиц совокупности.
Полученную по этой формуле величину округляют до целого числа, поскольку количество групп не может быть дробным числом.
При небольшом объеме информации (численности единиц в совокупности) число групп может быть установлено исследователем без использования формулы Стерджесса.
Величину интервала обычно округляют до целого (всегда большего) числа, исключение составляют лишь случаи, когда изучаются малейшие колебания признака (например, при группировке деталей по величине размера отклонений от номинала, измеряемого в долях миллиметра).
Нижнюю границу первого интервала принимают равной минимальному значению признака (чаще всего его предварительно округляют до целого числа); верхняя граница первого интервала соответствует значению (xmin + i). Для последующих групп границы определяются аналогично, то есть последовательно прибавляется величина интервала. Если единица обладает значением признака, равным величине верхней границы интервала, то ее следует относить к следующей группе.
Вариационный ряд, состоящий из двух граф (варианты и частоты), иногда дополняется другими графами, необходимыми для вычисления отдельных статистических показателей или для более отчетливого выражения характера вариации изучаемого признака. Достаточно часто в ряд вводится графа, в которой подсчитываются накопленные частоты (S). Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем данное значение, и исчисляются путем последовательного прибавления к частоте первого интервала частот последующих интервалов.
Частоты ряда (f) могут быть заменены частостями (w), которые представляют собой частоты, выраженные в относительных числах (долях или процентах) и рассчитанные путем деления частоты каждого интервала на их общую сумму, то есть:
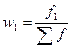
Замена частот частостями позволяет сопоставлять вариационные ряды с различным числом наблюдений.
Если вариационный ряд дан с неравными интервалами, то для правильного представления о характере распределения необходимо произвести расчет абсолютной или относительной плотности распределения.
Абсолютная плотность распределения (р) представляет собой величину частоты, приходящейся на единицу размера интервала отдельной группы ряда: р = f/i.
Относительная плотность распределения (р ') – частное от деления частости (w) отдельной группы на размер ее интервала: р '= w/i
Первым этапом изучения вариационного ряда является его графическое изображение. Дискретный вариационный ряд изображается в виде так называемого полигона, или многоугольника, распределения частот, являющегося разновидностью статистических ломаных. Для изображения интервального ряда применяются полигон распределения частот и гистограмма частот.
Строятся графики в прямоугольной системе координат. При построении полигона частот на оси абсцисс в одинаковом масштабе откладываются направо в порядке возрастания значения признака (для дискретного характера) или центральные значения интервалов (для интервальных рядов); по оси ординат наносится шкала для выражения величин частот. Из точек на оси абсцисс, соответствующих величине признака, восстанавливаются перпендикуляры высотой, соответствующей частоте; вершины перпендикуляров соединяются отрезками прямой. Крайние точки полученной ломаной соединяются с лежащими на оси абсцисс следующими (меньшими и. большими) возможными, но фактически не наблюдающимися значениями признака, частота которых, очевидно, равна 0. Замкнутая с осью абсцисс ломаная линия представляет полигон распределения частот.
Для построения гистограммы по оси абсцисс откладывают величины интервалов, а частоты изображаются прямоугольниками, построенными на интервалах с высотой в масштабе оси ординат. В случае неравенства интервалов гистограмма строится не по частотам или частостям, а по плотности распределения.
В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята),она особенно удобна для сравнения вариационных рядов. Накопленные частоты наносятся на чертеж в виде ординат; соединяя вершины отдельных ординат прямыми, получают ломаную линию, которая, начиная с нуля, непрерывно поднимается над осью абсцисс, до тех пор, пока не достигнет высоты, соответствующей общей сумме частот.
Если поменять местами оси координат в кумуляте, то получаем новый вид графического изображения – огиву.
При построении графических изображений вариационного ряда большое значение имеет соотношение масштабов по оси абсцисс (х) и оси ординат (у). В этом случае следует руководствоваться так называемым «правилом золотого сечения», в соответствии с которым высота графика должна быть примерно в два раза меньше его основания.
Для характеристики среднего значения признака в вариационном ряду применяются: средняя арифметическая, медиана, мода.
Средняя арифметическая для дискретного ряда распределения исчисляется по формуле:
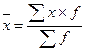
где x – варианты значений признака;
f – частота повторения данного варианта.
Средняя арифметическая для интервального ряда распределения:
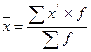
где x’ – середина соответствующего интервала значения признака;
Медиана (Me) соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы определяется ее номером:
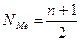
где п – число единиц в совокупности.
По накопленным частотам определяют ее численное значение в дискретном вариационном ряду.
Для характеристики размера вариации признака используются абсолютные показатели. К абсолютным показателям вариации относятся:
· размах колебаний;
· среднее линейное отклонение;
· среднее квадратическое отклонение;
· дисперсия;
· квартильное отклонение.
Размах колебаний (размах вариации)
R=xmax - xmin
где хmax, xmin - соответственно максимальное и минимальное значения признака. Величина показателя зависит от величины только двух крайних вариант и не учитывает степени колеблемости основной массы членов ряда.
Среднее линейное отклонение (d) и среднее квадратическое отклонение (σ) показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения. Среднее линейное отклонение определяется по формулам:
а) для несгруппированных данных (первичного ряда)
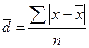
б) для п вариационного ряда
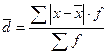
Среднее квадратическое отклонение (σ) и дисперсия (σ2) определяются так:
а) для несгруппированных данных
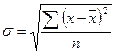 ;
; 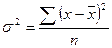
б) для п вариационного ряда
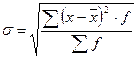 ;
; 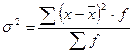
Формула для расчета дисперсии может быть преобразована. Дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины.
σ2 = х2 -(х)2.
Среднее квадратическое отклонение по своей величине всегда превышает значение среднего линейного отклонения в соответствии со свойством мажорантности средних.
Квартильное отклонение(dk) применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений:
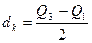
где Q3 Q1 соответственно третья и первая квартили распределения.
Дисперсия обладает рядом свойств, которые позволяют упростить расчеты.
1. Если из всех значений вариант отнять какое-то постоянное число А, то средний квадрат отклонений от этого не изменится.
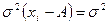
2. Если все значения вариант разделить на какое-то постоянное число А, то средний квадрат отклонений уменьшится от этого в А2 раз, а среднее квадратическое отклонение – в А раз:
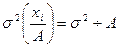
3. Если исчислить средний квадрат отклонений от любой величины А, которая в той или иной степени отличается от средней арифметической 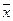 , то он всегда будет больше среднего квадрата отклонений
, то он всегда будет больше среднего квадрата отклонений 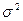 , исчисленного от средней арифметической:
, исчисленного от средней арифметической:
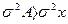
При этом средний квадрат отклонений будет больше на вполне определенную величину – на квадрат разности между средней и этой взятой величиной, то есть на 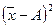 :
:
или 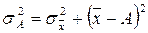
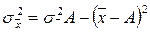
При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической используются относительные показатели вариации. Они вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане) и чаще всего выражаются в процентах.
Формулы расчета относительных показателей вариации следующие:
коэффициент осцилляции 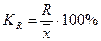 ;
;
относительное линейное отклонение 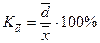 ;
;
относительный показатель квартильной вариации 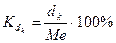 или
или 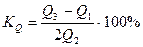
Наиболее часто применяется коэффициент вариации. Его применяют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
Изучая дисперсию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в расчетах, нельзя оценить влияние отдельных факторов, определяющих колеблемость индивидуальных значений (вариант) признака. Это можно сделать при помощи метода группировок, когда единицы изучаемой совокупности подразделяются на однородные группы по признаку-фактору. При этом кроме общей средней для всей совокупности исчисляются средние по отдельным группам (групповые или частные средние) и три показателя дисперсии:
· общая дисперсия;-
· средняя внутригрупповая дисперсия.
Величина общей дисперсии (σ02) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности, и определяется по формуле
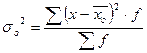
где х0 - общая средняя арифметическая для всей изучаемой совокупности.
Межгрупповая дисперсия (дисперсия групповых средних δ2) отражает систематическую вариацию, то есть те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки. Межгрупповая дисперсия определяется по формуле
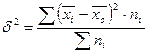
где 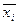 - средняя по отдельной группе;
- средняя по отдельной группе;
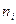 - число единиц в определенной группе.
- число единиц в определенной группе.
Средняя внутригрупповая дисперсия (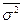 ) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.
) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.
Средняя внутригрупповая дисперсия определяется по формуле
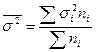 или
или 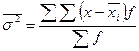
где 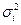 - дисперсия по отдельной группе;
- дисперсия по отдельной группе;
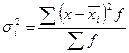
Указанные дисперсии взаимосвязаны между собой следующим равенством: величина общей дисперсии равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии:
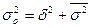
Это тождество отражает закон (правило) сложения дисперсий. Опираясь на это правило, можно определить, какая часть (доля) общей дисперсии складывается под влиянием признака-фактора, положенного в основу группировки.
Тема 6. Выборочное наблюдение: Несплошной учёт и ошибки репрезентативности. Способы отбора при выборочном наблюдении. Разновидности выборочного наблюдения. Принципы увеличения репрезентативности выборки. Экстраполяция данных выборочного наблюдения на генеральную совокупность.
Наиболее совершенным и научно обоснованным способом несплошного наблюдения является выборочное наблюдение. Выборочное наблюдение при строгом соблюдении условий случайности и достаточно большой численности отобранных единиц репрезентативно (представительно); по результатам изучения определенной части единиц с достаточной для практики степенью точности можно судить о всей совокупности. Однако вычисленные по материалам выборочного наблюдения статистические показатели не будут точно совпадать с соответствующими характеристиками для всей совокупности (генеральной совокупности). Величина этих отклонений называется ошибкой наблюдения.
Максимально возможная ошибка – это величина отклонения выборочной средней (доли) от генеральной, вероятность превышения которой вследствие случайных причин в условиях данной выборки очень мала.
Совокупность единиц, из которых производится отбор, принято называть генеральной совокупностью.
Совокупность отобранных единиц из генеральной совокупности называется выборочной совокупностью.
При выборочном анализе совокупности приняты следующие обозначения:
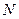 - объем генеральной совокупности (число входящих в нее единиц);
- объем генеральной совокупности (число входящих в нее единиц);
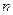 - объем выборочной совокупности (число единиц, попавших в выборку);
- объем выборочной совокупности (число единиц, попавших в выборку);
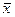 - генеральная средняя (среднее значение признака в генеральной совокупности);
- генеральная средняя (среднее значение признака в генеральной совокупности);
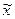 - выборочная средняя (среднее значение признака в выборочной совокупности);
- выборочная средняя (среднее значение признака в выборочной совокупности);
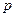 - генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности);
- генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности);
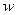 - выборочная доля (доля единиц, обладающих данным признаком в выборочной совокупности);
- выборочная доля (доля единиц, обладающих данным признаком в выборочной совокупности);
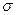 2 - генеральная дисперсия (дисперсия признака в генеральной совокупности);
2 - генеральная дисперсия (дисперсия признака в генеральной совокупности);
S2 - выборочная дисперсия (дисперсия признака в выборочной совокупности);
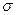 - среднее квадратическое отклонение признака в генеральной совокупности;
- среднее квадратическое отклонение признака в генеральной совокупности;
S - среднее квадратическое отклонение признака в выборочной совокупности.
Величина 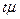 , обозначаемая ∆, называется предельной ошибкой выборки. Следовательно,
, обозначаемая ∆, называется предельной ошибкой выборки. Следовательно, 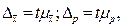
где 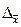 - предельная (максимально возможная) ошибка средней;
- предельная (максимально возможная) ошибка средней;
∆ 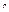 - предельная (максимально возможная) ошибка доли;
- предельная (максимально возможная) ошибка доли;
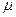 - величина средней квадратичной стандартной ошибки;
- величина средней квадратичной стандартной ошибки;
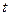 - коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки;
- коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки;
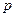 - вероятность.
- вероятность.
Формулы предельной ошибки позволяют решать задачи трех видов:
1. Определение пределов генеральных характеристик с заданной степенью надежности (доверительной вероятностью) на основе показателей, полученных по данной выборки.
Доверительные интервалы для генеральной средней:
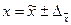 ;
; 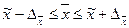 .
.
Доверительные интервалы для генеральной доли:
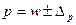 ;
; 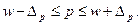
2. Определение доверительной вероятности того, что генеральная характеристика может отличаться от выборочной не более чем на определенную заданную величину.
Доверительная вероятность является функцией от t, определяемой по формуле: 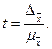
По величине t определяется доверительная вероятность.
3. Определение необходимого объема выборки, который с практической вероятностью обеспечивает заданную точность выборки.
По степени охвата единиц исследуемой совокупности различают большие и малые выборки. По способу формированиявыборочной совокупности различают следующие виды выборочного наблюдения: простая случайная (собственно случайная), типическая или районированная, серийная, механическая, комбинированная, ступенчатая, многофазная. Рассмотрим наиболее распространенные из них.
 2015-04-06
2015-04-06 1943
1943

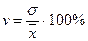 ;
;