При простой случайной выборке отбор единиц в выборочную совокупность производится непосредственно из всей массы единиц генеральной совокупности в форме случайного отбора, при котором каждой единице генеральной совокупности обеспечивается одинаковая вероятность (возможность) быть выбранной. Случайный отбор может быть проведен в двух формах: в форме возвратной (повторной) выборки и в форме безвозвратной (бесповторной) выборки. При повторном отборе вероятность попадания каждой единице генеральной совокупности остается постоянной, так как после отбора какой-то единицы она снова может быть выбранной. При бесповторном отборе выбранная единица не возвращается в генеральную совокупность и вероятность попадания отдельных единиц в выборку все время изменяется (для оставшихся единиц она возрастает).
Таблица 6.1
Формулы ошибок простой случайной выборки
| Показатель | Способ отбора единиц | |
| повторный | бесповторный | |
Средняя ошибка 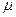 :
для средней :
для средней
| 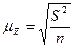
| 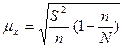
|
| для доли | 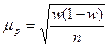
| 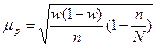
|
Предельная ошибка 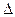 :
для средней :
для средней
| 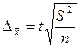
| 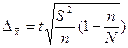
|
| для доли | 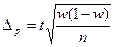
| 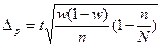
|
Таблица 6.2
Формулы для определения численности простой случайной выборки
| Показатель | Способ отбора единиц | |
| повторный | бесповторный | |
Численность выборки 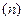 :
для средней :
для средней
| 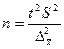
| 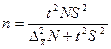
|
| для доли* | 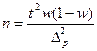
| 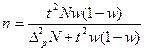
|
*В случаях, когда частность 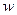 даже приблизительно неизвестна, в расчет вводят максимальную величину дисперсии, равную 0,25 (если даже приблизительно неизвестна, в расчет вводят максимальную величину дисперсии, равную 0,25 (если 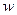 = 0,5, то = 0,5, то 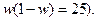
|
 2015-04-06
2015-04-06 335
335








