Теорема Вейерштрасса

Согласно второй теореме Вейерштрасса о непрерывных функциях, если функция f (x) непрерывна на отрезке [ a, b ], то она достигает на нем своей точной верхней и нижней грани.

Доказательство этой теоремы опирается на первую теорему Вейерштрасса, которая формулируется так:

Если функция f (x) непрерывна на отрезке [ a, b ], то она ограничена на нем, т.е. существует число M, такое, что| f (x)| ≤ M для всех x ∈ [ a, b ].

Возвращаясь ко второй теореме Вейерштрасса, обозначим через M точную верхнюю грань множества значений функции (или наибольшее значение функции) на отрезке [ a, b ]. Предположим противное − что точная верхняя грань не достигается, т.е. допустим, что

f (x) < M ∀ x ∈ [ a, b ].

Рассмотрим вспомогательную функцию:

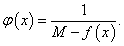
Поскольку знаменатель не равен нулю, то функция φ (x) также непрерывна на [ a, b ] и, следовательно, по первой теореме Вейерштрасса ограничена на этом отрезке: φ (x) ≤ L, где L > 0. Отсюда получаем, что

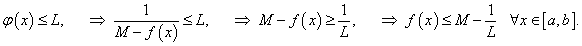
Другими словами, число 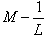будет являться точной верхней гранью функции f (x), что противоречит условию. (По условию, точная верхняя грань функции равна M.)

Таким же образом можно доказать, что непрерывная на отрезке [ a, b ] функция достигает свой точной нижней грани (или наименьшего значения).

Итак, согласно второй теореме Вейерштрасса, непрерывная на отрезке функция всегда достигает своего наибольшего и наименьшего значения на этом отрезке.