Необходимое условие перегиба

Сформулируем необходимое условие перегиба графика функции.

Пусть график функции y=f(x) имеет перегиб в точке 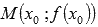и имеет при 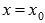непрерывную вторую производную, тогда выполняется равенство .

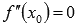Из этого условия следует, что абсциссы точек перегиба следует искать среди тех, в которых вторая производная функции обращается в ноль. НО, это условие не является достаточным, то есть не все значения 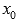, в которых вторая производная равна нулю, являются абсциссами точек перегиба.

Еще следует обратить внимание, что по определению точки перегиба требуется существование касательной прямой, можно и вертикальной. Что это означает? А означает это следующее: абсциссами точек перегиба могут быть все 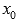из области определения функции, для которых 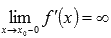и . Обычно это точки, в которых знаменатель первой производной обращается в ноль.