Первое достаточное условие перегиба

После того как найдены все 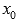, которые могут быть абсциссами точек перегиба, следует воспользоваться первым достаточным условием перегиба графика функции.

Пусть функция y=f(x) непрерывна в точке 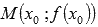, имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки 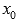. Тогда, если в пределах этой окрестности слева и справа от 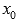, вторая производная имеет разные знаки, то 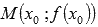является точкой перегиба графика функции.

Как видите первое достаточное условие не требует существования второй производной в самой точке 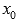, но требует ее существование в окрестности точки .

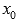Сейчас обобщим всю информацию в виде алгоритма.