Среднее значение в интервальном ряду распределения рассчитывается по формуле средней арифметической взвешенной:
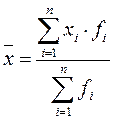 ,
,
где xi –середина интервала усредняемого показателя;
n – число единиц (объем) совокупности;
fi – частота, которая показывает как часто встречается значение признака в статистической совокупности.
Таблица 3 –Вспомогательная таблица для расчета средней арифметической величины по объему кредитных вложений
| № п/п | Группы банков по объему кредитных вложений, млн. руб. | Число банков, fi | Середина интервала, xi’ | xi’·fi | Накопленная частота, S |
| 64-264 | |||||
| 265-465 | |||||
| 466-666 | |||||
| 667-867 | |||||
| 868-1068 | |||||
| 1069-1269 | |||||
| Итого | - | - | - |
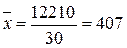 (млн. руб.)
(млн. руб.)
Таким образом, средний объем кредитных вложений среди банков, представленных в выборочной совокупности, составляет 407 млн. руб.
Для характеристики структуры вариации рассчитывают структурные средние моду и медиану.
Мода – значение признака, которое наиболее часто встречается в ряду распределения. Для интервального ряда мода определяется по наибольшей частоте. Мода находится по формуле:
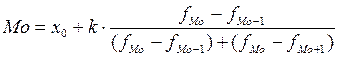 ,
,
где x0 – нижняя (начальная) граница модального интервала;
k – величина интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
Медиана – значение признака, которое делит совокупность на две равные части, т.е. 50% единиц совокупности имеют значение меньше медианы, а остальные – больше медианы.
Для определения медианы рассчитывается ее порядковый номер по формуле:
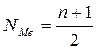 ,
,
где n – число единиц совокупности.
Затем рассчитывается накопленные частоты. После смотрят, какая из накопленных частот впервые превышает номер медианы. Медиану рассчитывают по формуле:
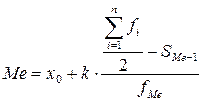 ,
,
где x0 – нижняя граница медианного интервала;
k – величина интервала;
∑f = n – число единиц совокупности;
SMe-1 – накопленная частота (кумулятивная частота) интервала, предшествующего медианному;
fMe – медианная частота.
Степень близости данных отдельных единиц совокупности к средней величине измеряется рядом абсолютных и относительных показателей вариации.
К абсолютным показателям вариации относятся:
¾ размах вариации; среднее линейное отклонение;
¾ дисперсия; среднее квадратическое отклонение.
Размах вариации представляет собой разность между максимальным и минимальным значениями признака совокупности, и находится по формуле:
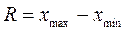
Среднее линейное отклонение представляет собой среднюю величину из отклонений значений признака от их средней величины, которое рассчитывается по формуле: 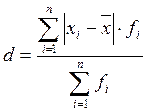
Таблица 4 – Вспомогательная таблица для расчета показателей вариации по объему кредитных вложений.
| № п/п | Группы банков по объему кредитных вложений, млн. руб. | Число банков, fi | Середина интервала, xi’ | 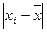
| 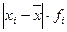
| 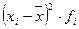
|
| 64-264 | ||||||
| 265-465 | ||||||
| 466-666 | ||||||
| 667-867 | ||||||
| 868-1068 | ||||||
| 1069-1269 | ||||||
| Итого | - | - |
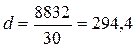 (млн.руб.)
(млн.руб.)
Таким образом, средняя величина из отклонений значений объема кредитных вложений от их средней составляет 294,4 млн. руб.
Дисперсия – это средний квадрат отклонений индивидуальных значений признака от их средней величины. Дисперсия находится по формуле:
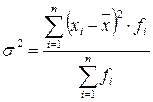
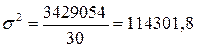 (млн.руб.)2
(млн.руб.)2
Таким образом, средний квадрат отклонений индивидуальных значений объема кредитных вложений от их средней величины составляет 114301,8 млн. руб.2
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии, т.е. корень квадратный из среднего квадрата отклонений индивидуальных значений признака от их средней величины. Среднее квадратическое отклонение находится по формуле:
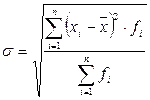
Найдем среднее квадратическое отклонение по объему кредитных вложений:
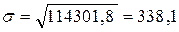 (млн. руб.)
(млн. руб.)
Относительные показатели вариации в общем виде показывают отношение абсолютных показателей вариации к их средней величине.
К относительным показателям вариации относятся:
¾ коэффициент осцилляции;
¾ относительное линейное отклонение;
¾ коэффициент вариации.
Коэффициент осцилляции находится по формуле:
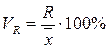
Коэффициент осцилляции для выборки по объему кредитных вложений равен:
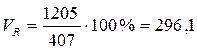 %
%
Относительное линейное отклонение рассчитывается по формуле:
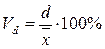
Относительное линейное отклонение для выборки по объему кредитных вложений равно:
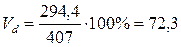 %
%
Коэффициент вариации характеризует однородность совокупности. Совокупность считается однородной, если коэффициент вариации меньше либо равен 33%, иначе признается неоднородной. Коэффициент вариации определяется по формуле:
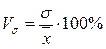
Тогда, коэффициент вариации для выборки по объему кредитных вложений равен:
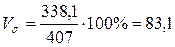 %
%
Коэффициент вариации для выборки по объему кредитных вложений больше, чем 33% (равен 83,1%), следовательно, совокупность неоднородна, а это означает, что среднее значение признака не является центром распределения.
 2015-04-06
2015-04-06 522
522








