Пусть f(x) - периодическая функция, с периодом Т=2π, отвечающая условиям Дирихле. Тогда она может быть представлена рядом Фурье:
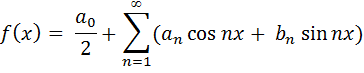
где коэффициенты ряда Фурье для периодической функции f(x) с Т=2π вычисляются в соответствии с формулами (4.3):
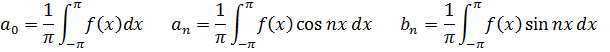

Воспользуемся показательной и тригонометрической формами комплексного числа 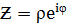 и Z= ρ cos φ + iρ sin φ.
и Z= ρ cos φ + iρ sin φ.
Приравняем эти выражения.
Тогда: 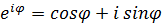 , поменяем φ на –φ
, поменяем φ на –φ
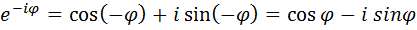
Сложим два последних выражения:
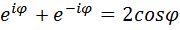 ,т.е.
,т.е. 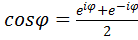 (4.14)
(4.14)
После вычитания второго выражения из первого в итоге получим:
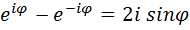 , т.е.
, т.е. 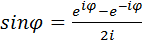 (4.15)
(4.15)
Формулы (4.14) и (4.15) называются формулами Эйлера. Используем их для выражения (простой гармоники) общего члена ряда Фурье
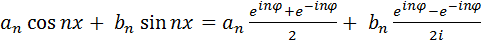 . Домножим числитель и знаменатель второго слагаемого на i (избавимся от мнимости в знаменателе).
. Домножим числитель и знаменатель второго слагаемого на i (избавимся от мнимости в знаменателе).
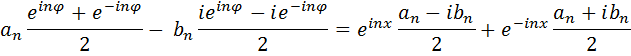
Тогда общий член ряда Фурье запишется в виде:
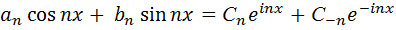
Обозначим 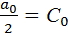
Очевидно тогда, что сумма N членов ряда Фурье для функции 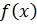 может быть записана в виде:
может быть записана в виде:
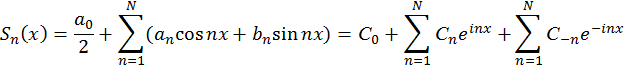
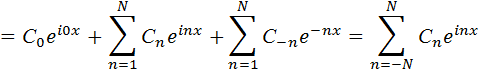
При N 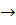 ∞, получим:
∞, получим:
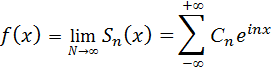 (4.16)
(4.16)
Если предел существует, то ряд сходиться для данного значения x.
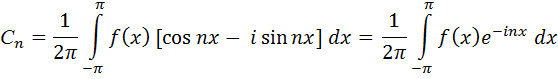 n=1,2,3…
n=1,2,3…
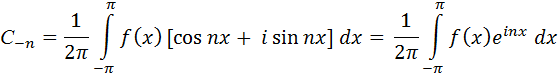
По другому можем записать так:
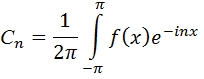 (4.17)
(4.17)
где n= ±1, ±2, ±3, …
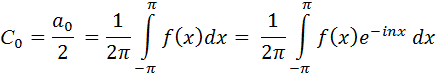
где n=0
Зная коэффициенты комплексного ряда Фурье, формулы (4.16) и (4.17), можно найти коэффициенты действительного ряда Фурье для той же функции
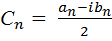 ,т.е.
,т.е. 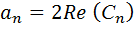 , bn =-2Im (Cn)
, bn =-2Im (Cn)
Пример: разложить заданную функцию в ряд Фурье в действительной и комплексной формах
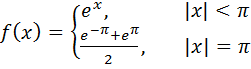
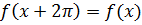
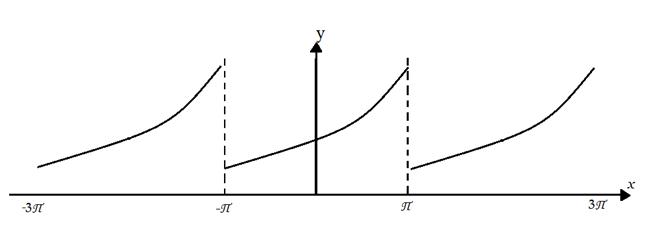
рис. 4.4
Функция 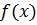 отвечает условиям Дирихле: имеет период 2π; на отрезке [-π; π] (длиной в период) функция ограничена; непрерывна и монотонна.
отвечает условиям Дирихле: имеет период 2π; на отрезке [-π; π] (длиной в период) функция ограничена; непрерывна и монотонна.
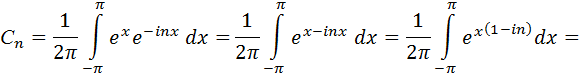
 |
|
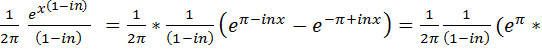
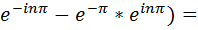
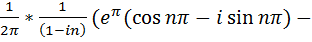
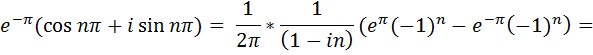
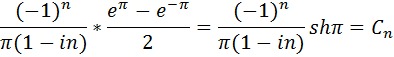
При вычислениях учитывали, что cos nπ= (-1)?; sin nπ= 0,
т.е.
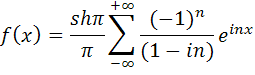
(Подробнее о гиперболических функциях следует посмотреть в «Приложении»). Перейдем к действительной форме ряда Фурье для заданной функции:
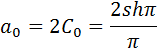
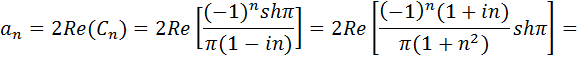
= 2?(-1)??shπ /(π(1+n²))
bn = -2?Im(Cn) = -2n?(-1)??shπ/(π(1+n²))
Окончательно получим:
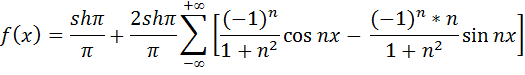
Пример: записать ряд Фурье в комплексной форме для периодической функции f(x)=ex (период T=2 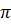 ), определенной при 0<x<2
), определенной при 0<x<2 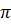 . Воспользуемся формулами (4.16) и (4.17).
. Воспользуемся формулами (4.16) и (4.17).
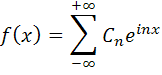
где
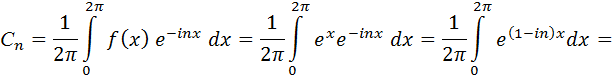

| |
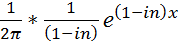 =
= 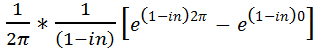 =
=
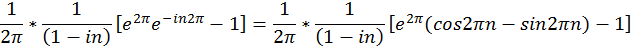
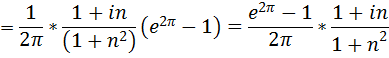
(n=0, 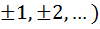
Тогда
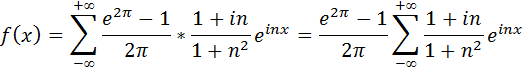
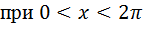
Пример: от комплексной формы ряда Фурье, полученной в предыдущей задаче перейти к действительной форме ряда Фурье.
Т.к. 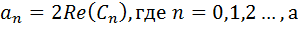
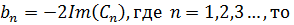
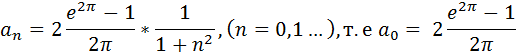
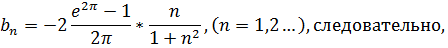
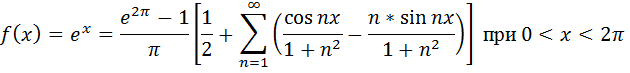
Пример: записать ряд Фурье для периодической (T=2π) функции 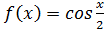 , на интервале [-π
, на интервале [-π 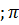 ] в комплексной форме.
] в комплексной форме.
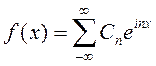 , где
, где 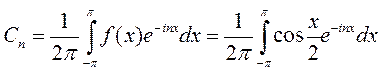
Воспользуемся формулой Эйлера: 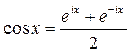
тогда 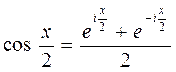 , следовательно,
, следовательно,
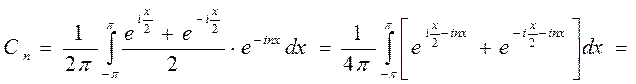
= 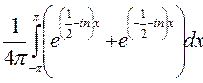 =
= 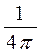
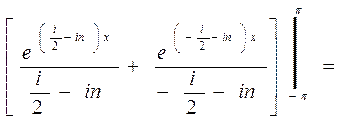
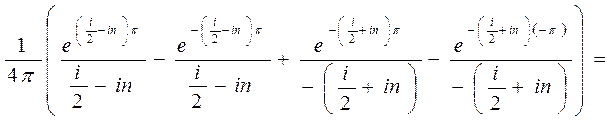
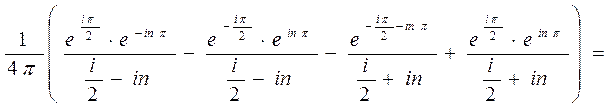
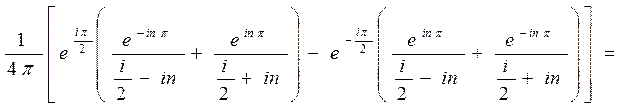
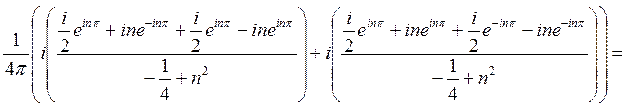
 =
= 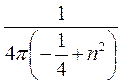
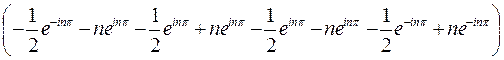 =
=
= 
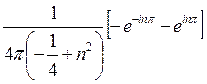 =
= 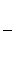

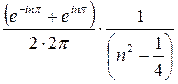 =
= 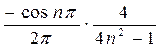 =
= 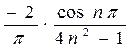 =
=
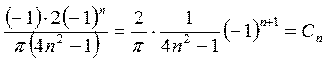
При этом учли, что:
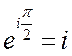
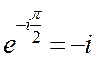 , а
, а 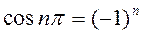
Тогда 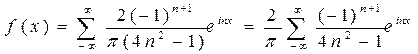
От комплексной формы ряда Фурье перейдем к действительной форме. Т.к. 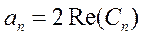 , где n=0,1,2.., то
, где n=0,1,2.., то
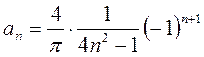 ;
; 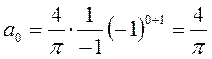
bn= - 2Im(Cn) но Im(Cm)=0, т.е. ряд Фурье в действительной форме примет вид:
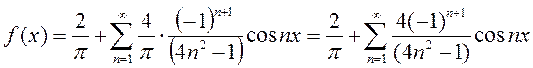
Комплексная форма ряда Фурье периодической функции периода 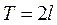
Пусть 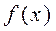 - периодическая функция периода
- периодическая функция периода 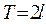 , удовлетворяющая условиям Дирихле. Тогда подстановка
, удовлетворяющая условиям Дирихле. Тогда подстановка 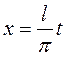 приводит к функции
приводит к функции 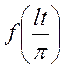 , разложимой в ряд Фурье с периодом 2
, разложимой в ряд Фурье с периодом 2 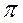 . Тогда для такой функции имеем:
. Тогда для такой функции имеем:
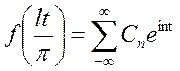 , где
, где 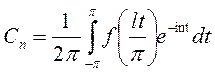
Сделаем обратный переход к аргументу 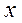 с помощью подстановки
с помощью подстановки 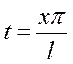 . Получим комплексную форму ряда Фурье для периодической функции
. Получим комплексную форму ряда Фурье для периодической функции 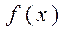 с периодом T= 2l.
с периодом T= 2l.
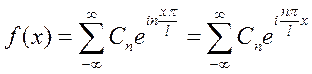
При этом
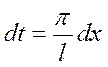 ,
, 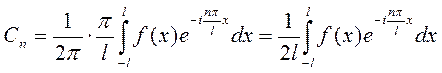

 2015-04-08
2015-04-08 16893
16893
