Рассмотрим одну из первых по времени «классических» задач теории массового обслуживания; эта задача возникла из практических нужд телефонии и была решена в начале нашего века датским математиком Эрлангом. Задача ставится так: имеется n каналов, на которые поступает поток заявок с интенсивностью λ. Поток обслуживания одним каналом имеет интенсивность μ (величина, обратная среднему времени обслуживания tob). Найти финальные вероятности состояний СМО, а также характеристики ее эффективности:
А – абсолютную пропускную способность, то есть среднее число заявок, обслуживаемых в единицу времени;
Q – относительную пропускную способность, то есть среднюю долю пришедших заявок, обслуживаемых системой;
Ротк - вероятность отказа, то есть того, что заявка поки-нет СМО необслуженной;
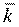 – среднее число занятых каналов.
– среднее число занятых каналов.
Состояние системы массового обслуживания S будем нумеровать по числу заявок, находящихся в системе (в дан-ном случае оно совпадает с числом занятых каналов):
S0 – в СМО нет ни одной заявки;
S1 - в СМО находится одна заявка (один канал занят, остальные свободны);
Sk - в СМО находится k заявок (k каналов заняты, остальные свободны)
Sn - в СМО находятся n заявок (все n каналов заняты).
Граф состояний СМО выглядит следующим образом:
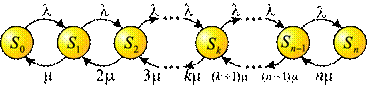
Найдем Potk - вероятность того, что пришедшая заявка получит отказ. Для этого нужно, чтобы все n каналов были заняты, значит,
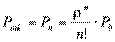
Отсюда находим относительную пропускную способность - вероятность того, что заявка будет обслужена:
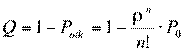
Абсолютную пропускную способность получим, умножая интенсивность потока заявок 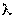 на Q:
на Q:
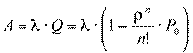
Таким образом, мы нашли интенсивность потока обслуженных системой заявок. Так как каждый занятый канал в единицу времени обслуживает в среднем 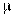 заявок, то среднее число занятых каналов равно
заявок, то среднее число занятых каналов равно
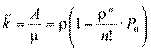
 2015-04-08
2015-04-08 5356
5356








